√画像をダウンロード 距離 時間 速度 公式 398738

等加速度直線運動2つの公式確認 等加速度直線運動では速さと変位（移動距離）の2つの公式がありました。 速度が一定に増加（減少）するので 初速度 \(v_0\) で加速度 \(a\) とすると 時刻 \(t\) における つまり 時速60キロ は1時間に60キロメートル進むことができる速さということになります。 速さ60 = 距離(60km) ÷ 時間(1h) 60km/hなどと表記されている場合『／』は割り算を意味しますので、単位だけ見てみると 速さ ＝ km/h となるのです。 さらに覚えやすくするために図を見ていき 等加速度運動の3公式 まず，等加速度運動とは読んで字のごとく各方向で加速度が一定である運動のことです。 速度と加速度，また運動を記述するにあたり必要な時間の導入については こちらのページ を参考にしてください。 教科書にも出てくる重要な

速率公式

距離 時間 速度 公式

距離 時間 速度 公式- みなさんこんにちは！今回は，力学の基本になる速度と移動距離のお話． 速度とは？ 日本語で言えば，決まった時間でどれくらい進めるかってこと． この時「方向も考える」のが速度 ．方向の概念なしに数字の大きさだけでいいのは「速さ」． 要推出这公式，不难。 我就不说积分什么的，一是你未必能看明白，二是我自己也没有学好。 首先，这是一个匀变速的直线运动，要求距离，可以利用距离=速度*时间 有了加速度跟时间，就能求出平均速度： V末=VoaT,V平=(V末Vo)/2 即V平=VoaT/2 所以：x=v0t1/2*at^2

考虑空气阻力的自由落体 下落的时间和的公式是什么 球体自由落体空气阻力公式 人社网

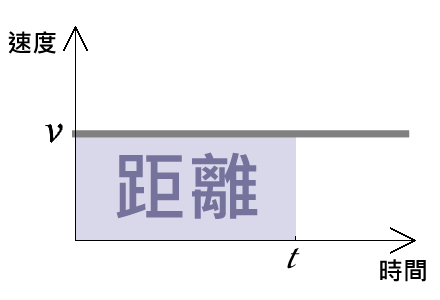
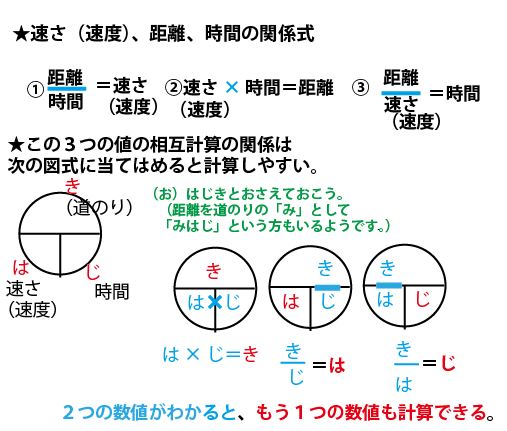
 小学校などで, き・は・じの公式 も習いますが,公式の暗記より,なぜそういう計算をするのか,仕組みを理解することがはるかに重要です さて,60÷15をすると車の速さは, 40km/h だと分かります ここで,距離と速度と時間の関係を考えてみましょうボールの速度は次の公式で求められる。 v = gt v 速度 t 時間 距離 上のような速度ー時間グラフでは、面積は距離を表します。 上図のように速度が変わらない場合、距離（ボールが動いた距離）は速度×時間で求められます。これはグラフでいうと面積に各記号の意味を理解しましょう。 V i は「初速度」です。 V f は「速度」です。 t は「時間」です。 d は「距

行星與太陽的連線，在相同時間，掃過相同面積。 2 『面積速率』的意義： t A Δ Δ ：單位時間，太陽與行星的連線，掃過的面積 近日點the perihelion；遠日點the aphelion 3 推導前的數學背景知識： 三角形面積公式 扇形面積公式 4 數學推導：1 時間判斷：(題目中常出現的文字!) 2 鉛直上拋運動的對稱性： (1) 上升至最高點與由最高點下拋至拋出點所需 時間相同→推論：不論上升或下降相同高度， 其所需時間相同。 (2) 在同一高度處，上升與下降的瞬時速度大小相 等，方向相反。 3它同時顯示速度（指大小）和方向 一部分的樂它的維數為 lt1我們可以通過距離時間圖的斜率來確定 您如何僅使用位置與時間圖並且沒有給出方程來找到瞬時速度

等速度運動（速度を計算） 等速度運動（移動距離を計算） 等速度運動（所要時間を計算） 等速度運動（往復の平均速度） 遠心力 回転速度 等加速度運動（加速度を計算） 等加速度運動（所要時間を計算） トルク、回転数、出力の計算速度、時間、距離の値が分かっている場合、次の公式が使えます。 初速度： V i = 2(d/t) V f;時速4kmで3時間歩いたら、どれだけの距離を移動したか？ という問題にも、計算で解答できます。 この場合は、 速さ × 時間 = 距離 になります。 今回は、距離の単位はkm (キロメートル)、時間はh (時間)で固定しています。 学校の課題などでは、距離の

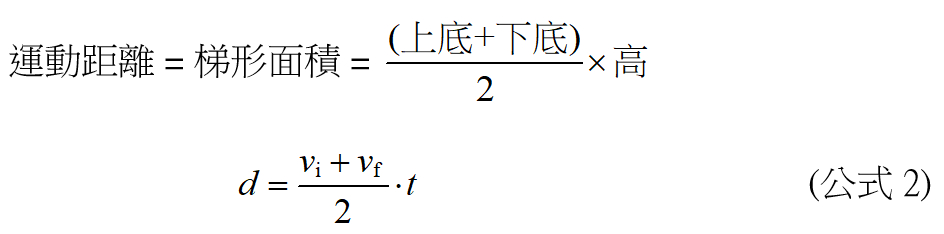
如何看懂物理公式 三 以數學運算取代邏輯推理 台灣物理學會 物理雙月刊

怎么计算初速度 生活百科

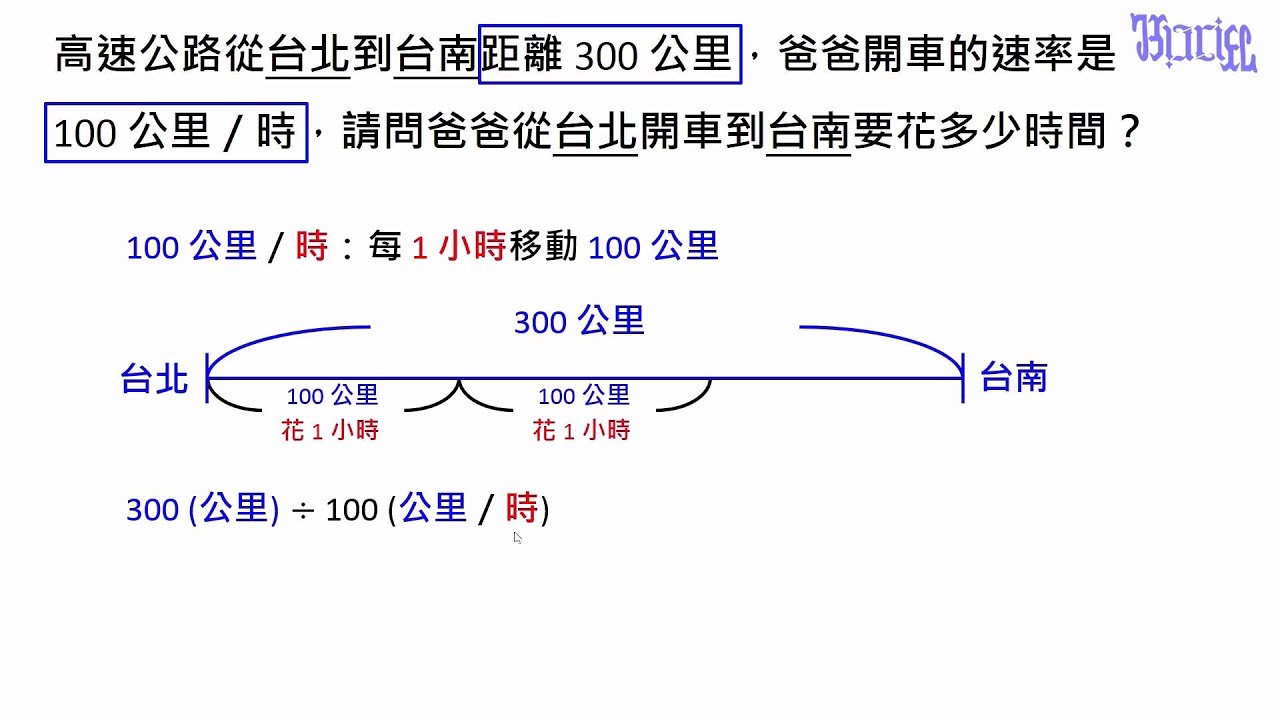
 出発地から目的地までの距離(変位) Δx ＝ x 2 － x 1 、かかった時間 Δt ＝ t 2 － t 1 ですね。 (Δ (デルタ)は差分や変化量を表すギリシャ文字) そうすると、平均の速度\(\bar{v}\)＝\(\frac{変位}{時間}\)と、普通の速度の公式と同じように計算できますよ。停止距離＝空走距離＋制動距離 速度の2乗に 比例して大きく 衝突回避の 可能性は小さく ※Speed management –A road safety manual for decisionmakers and practitioners –より 速度による停止距離時間を求める 時間を求めたいときには、 時間＝距離 ÷ 速さ という公式を使います。 例えば、距離 30 k m の道のりを、時速 5 k m で進んだときにかかる時間は、 距離 ÷ 速さ = 30 ÷ 5 = 6 つまり、 6 時間 です。 公式を忘れても、はじきの図で求めたい

13光武國小五年八班 14六年八班 十一月14

速率 10 距離 速率 時間 Youtube

距離と時間に関する公式 s＝vo t＋1at 2 vo：初速度 s：距離 2 t：時間 a：加速度 物体の位置sは、このように決まります。 問題 物体を下に5m／sで投げた。物体の加速度は10m／s 2 として 7秒後の物体の距離を求めよ 解答 s＝vo t＋1／2 at 2 2 ＝35＋245 ＝280m 速度と使用公式從距離和時間計算平均速度 通過距離和時間計算平均速度，以下公式可以為您提供幫助。 1。請輸入以下公式： =a2/(b2*24) 放入要輸出結果的空白單元格，然後將填充手柄向下拖動到要獲取所有結果的單元格，請參見屏幕截圖： 備註：在以上公式中， a2 是距離 b2 是時候了，請根據需要更改 初速度为0时的基本公式：S位移；a加速度；t 时间； v：速度 S=½ a t² （物体从0开始，加速运动，到t时刻所运行的距离） v=at （ 物体从0开始，加速运动，到t时刻所达到的速度） 初速度为v0时的基本公式： S=½ a t²v0*t （物体从V0开始，加速运动，到t时刻所运行

上距離速度時間 ニスヌーピー壁紙

等距离平均速度公式 扒拉扒拉

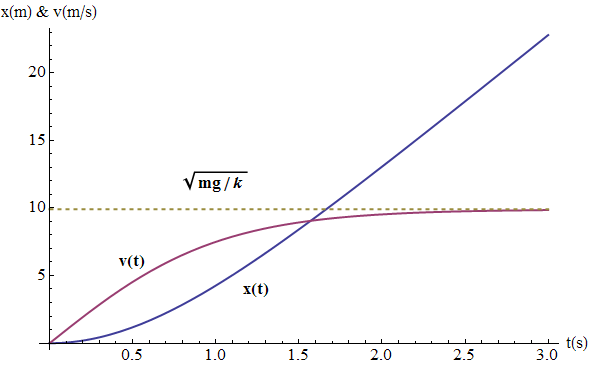
 截至目前為止，在定義了速度與加速度之後，我們只透過代學裡的 移項運算 以及 面積計算 ，便得出了三個重要的運動學公式，用以描述物體在等加速度運動下的情況。 萬一我們不知道運動的時間呢？ 現在，我們來看一個簡單的生活實例，假設我們拿一個網球，如圖六 (a) 所示，讓它從胸口的高物理公式總表 運動學 直線運動 速度 平均速度== 平均速率v== 只有大小沒有方向的物理量(純量) 瞬時速度==極短時間內的平均速度 瞬時速率v==極短時間內的平均速率 加速度速度vと時間tの関係を表すグラフのこと 速度v s 速度v 時間t 時間 グラフの面積sを求めると、面積＝縦×横＝ 速度×時間となるが、速度×時間＝距離なので、 vtグラフの特徴① vtグラフにおいて面積は距

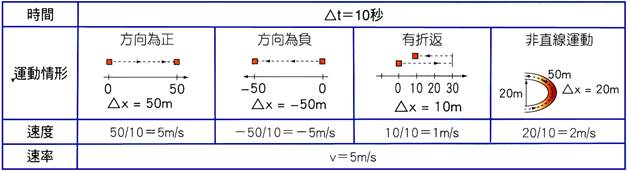
一

平均速率 紀算 補習班 數學補習班 三重 文理補習班 數學公式 數學題庫 數學競賽 國小數學 國中數學 痞客邦

P = W t W又は J/s 動力= (トルク×回転角)÷時間 P = T × θ t W又は J/s 動力=トルク×角速度 P = T × ω W 又は J/s 回転速度 N rpmの場合の公式 動力 トルク 回転速度 ･ 動 力 = ト ル ク × 2 π × 回 転 速 度 60 P = T ･ 2 π N 60 ≒ T N 9549 W又は J/s 工学単位を等加速度運動の速度の公式は、初速度 のまま同じ速度で直線運動をしてるから、 と表されることが分かります。 速度というのは単位時間1秒当たりの変位の変化なので、 秒たった後に進んだ移動距離 は、速度に時間 をかければいいです。 というわけで1：速度と時間に関する公式 ・vは 加速した後の速度 ・v₀は加速する前の速度（ 初速 ） ・aは 加速度 （単位はm/s²) ・tは 時間 （単位は秒） 問題をみながら使い方を考えてみましょう。 問題 秒速5mで走っていた自転車が、10秒後に秒速10mに加速を

行程赶路一会快一会慢 用等距平均速度公式秒解答案

距离和速度的关系公式 搜狗搜索

こで、速度は v (t)= gt というように時間に比例して増大する。物体の移動距離は、速度が一定なら速 度 時間となるが、速度が時間に比例して変化する場合には加速度 時間 時間 2 となる。すなわち、 x (t)= 1 2 gt 2 32 仕事とエネルギー 日常用語の「仕事速度の公式 速度=進んだ距離÷かかった時間 進んだ距離：1km かかった時間：2時間 → 1÷2=60 → 1時間当たり60km進んでいる → 時速60km 算数問題では、問題と答えで単位が違うこともあるので注意してください。 進んだ距離：1km 加速度 a ＝(速度の変化量 Δv)÷(時間 Δt)＝(90 m/s－30 m/s)÷(40 s－10 s)＝ m/s 2 (メートル毎秒毎秒) 確かに、10 sごとに速度は m/sずつ増えていますね。 理解を深めるために、この運動をグラフにしてみましょう！ 等加速度直線運動のグラフと速度を求める公式

六年级科学如何计算速度 A Star Academy Learning Centre 精英教育中心 Facebook

用距離速率時間公式解決問題

 速さ 時間 = ( 距離 ÷ 時間 ) 時間 速さ 時間 = 距離 2の公式が完成 しました。 この式の 両辺を 速さ で割る と、 速さ 時間 ÷ 速さ = 距離 ÷ 速さ 時間 = 距離 ÷ 速さ つまり、単位から 1 が分かれば、 重要3公式は覚える必要がありません 。公式：速率*時間=距離 1輸入速率 Km/h 公里/時 m/min 公尺/分 cm/s 公分/秒 2輸入時間 h小時 min分 sec秒 3 計算結果如下等速度運動（速度を計算） 110 /90件 表示件数 5 10 30 50 100 0 1 26 歳未満 / 小・中学生 / 非常に役に立った / 使用目的 自転車の平均速度 ご意見・ご感想 毎日1秒でも速く学校に行けるようにタイムを測って平均時速を出すために使いました。

高一高二必備 高中物理重點 考點都在這兒 6 壹讀

第43天運動 平均速度與瞬時速 每日頭條

まず公式の意味を確認していきましょう。 ① v ＝ v0 ＋ at について これは，初速度 v0 ，加速度 a で等加速度直線運動している物体が，時刻 t にどのような速度 v になっているのかを表しています。 一般には速度を求めるときに使いますが， v ， v0 ， a

加速度公式距离加速度时间距离计算公式 尚书坊

速度換算方法速度 Sed

里程計算距離 時間 速率計算機 計算pro Wrmzko

自由落體公式時間計算公式 超卓工業股份有限公司 Bsmba

巧用公式解决多次相遇问题

距離 時間 速率 計算機 蘋果健康咬一口

時速公式時間 距離 速度 Rzcpe

路程計算 Smitten

速率時間距離公式已知加速度 時間 求距離的公式是什么 怎么導出的 百 Tfdvy

1

自由落體公式重量自由落體到地面的重量怎樣計算 Rjhi

如何寻找速度 有妙招

速率公式

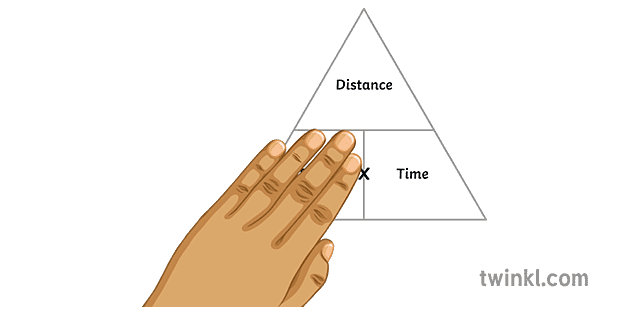
速度覆盖的金字塔数学距离时间公式三角形二次 Illustration

國立臺中教育大學數學教育學系國小教師在職進修教學碩士班碩士論文指導教授 胡豐榮博士ss 分析法應用於國小速度概念文字題之研究研究生

高等数学 速度 路程 时间公式 Qq 44的博客 Csdn博客

计算平均速度 提示 21

書報討論 國小數學教材分析 時間與速率 指導教授 葉啟村老師研究生 辛綺秀學號 Ppt Download

速度 速率 追趕問題 Lessons Blendspace

如何找到时间 知道距离和速度 自然科学21

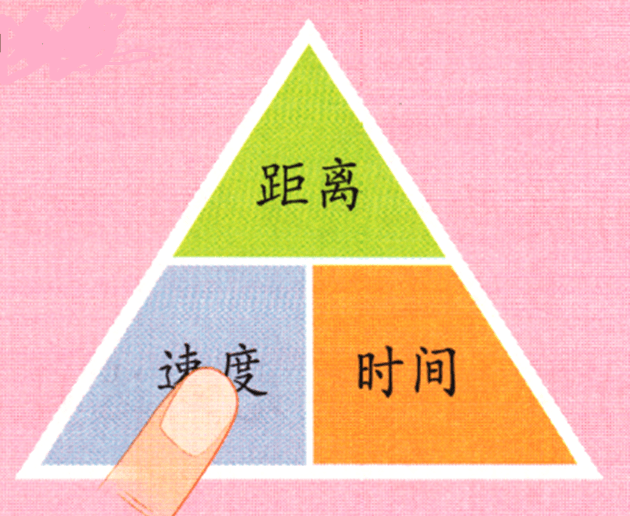
科学速度2 Science Quiz Quizizz

6年级单元七 速度的计算 Youtube

如何在excel中根據距離和時間計算平均速度

時間公式

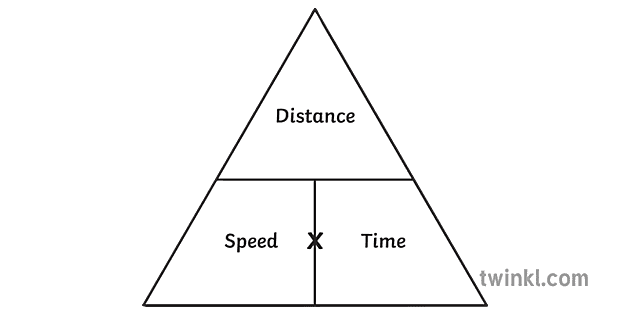
距離速度時間金字塔數學公式三角形次級黑白rgb Illustration

小学数学公式大全挂图墙贴图形面积常用公式表小学生三四五六年级

为什么当速度趋于光速时 无论多远的距离 都能瞬间到达 全网搜

例題 速率的三個公式應用1 速率 距離 時間 數學 均一教育平台

速率教學速率與速度 Pripdw

以最通俗的方式讲解爱因斯坦 相对论 小学生都能听懂 理解 黑点红黑点红

林肯文理補習班 專收青溪國中 小六第二次段考速率單元孩子們常常因為應用問題的文字而搞不清楚題意 Facebook

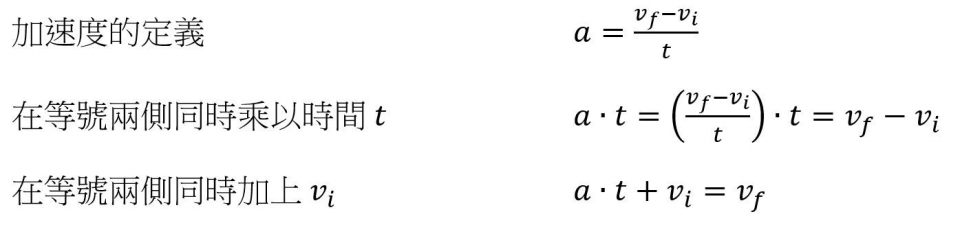
如何看懂物理公式 三 以數學運算取代邏輯推理 台灣物理學會 物理雙月刊

最も選択された 距離時間速度 ニスヌーピー壁紙

觀念 速率公式 數學 均一教育平台

加速度公式距离加速度时间距离计算公式 尚书坊

物理 点点教你怎么用公式 1 知乎

Hznppp99pdks2m

测量平均速度 机械运动ppt免费课件 第一ppt

物理时间公式 在物理中求时间速度距离的公式用字母怎么表示 三人行教育网 Www 3rxing Org

1

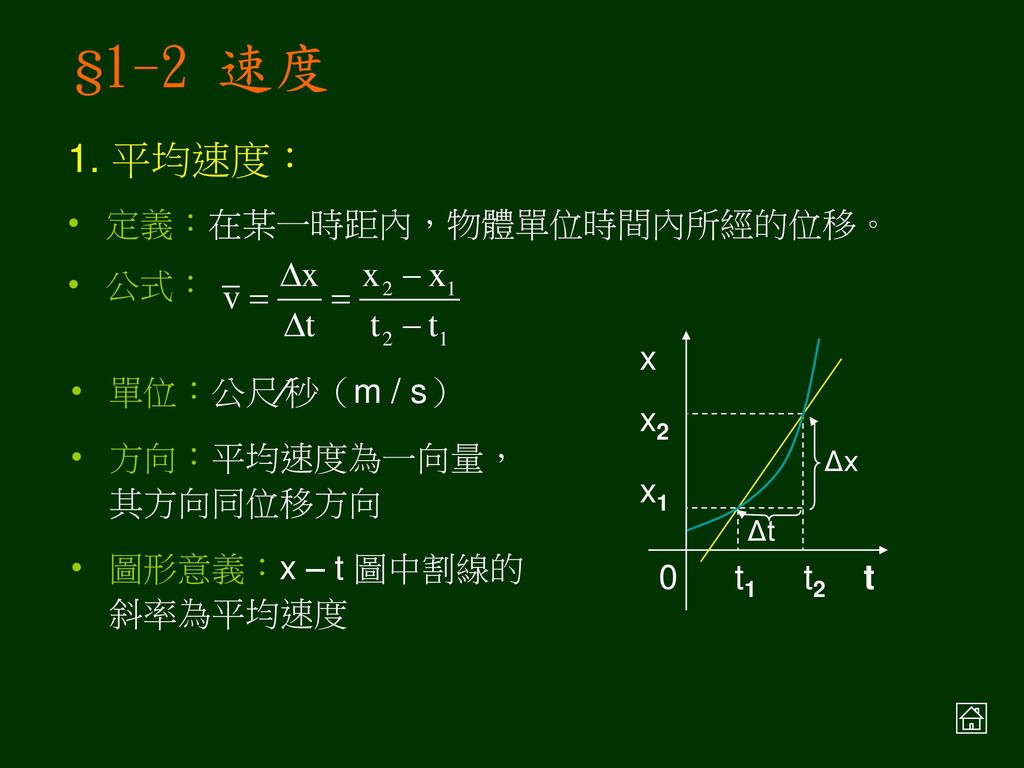
直線運動 1 1 位移 1 2 速度 1 3 加速度 1 4 等加速度直線運動 1 5 自由落體 1 6 光滑斜面上的運動 Ppt Download

六年级科学 速度 Youtube

速率換算 測試 網路連線速度測試 Steur

关于光速 有个问题困扰了很久了 职场资讯 存满娱乐网

路程的远近 速度的快慢 时间的多久之间关系的问题称为行程问题 哔哩哔哩

問題探討 愛因斯坦的相對論的確錯了

斜抛与平抛水平位移 距离水平面高度相同的一点 速度大小相同的斜抛运动与平抛运动 水平位移哪个大 如何推导 三人行教育网 Www 3rxing Org

3

時速公式時間 距離 速度 Rzcpe

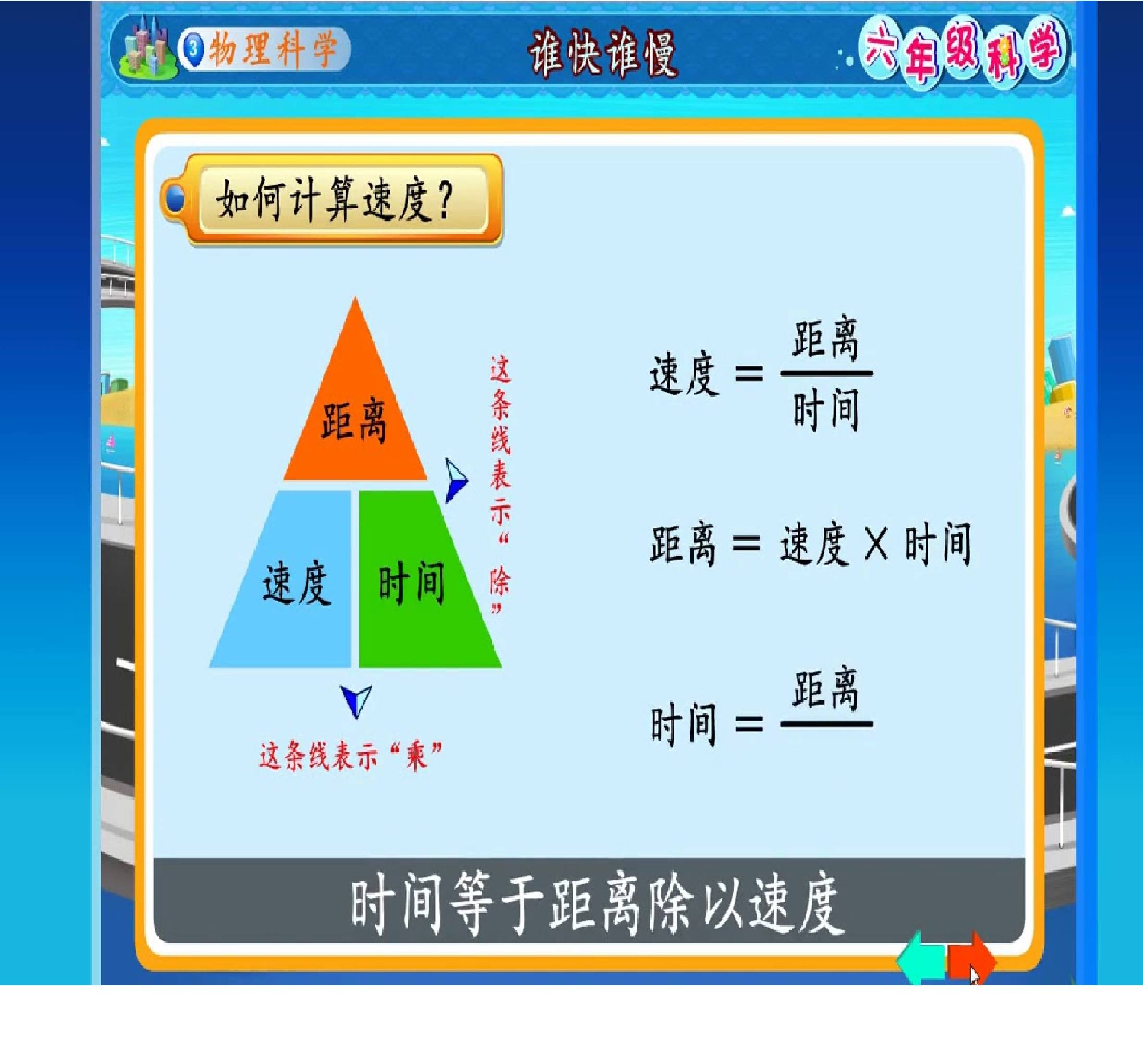
六年级科学第七课速度 Science Quiz Quizizz

如何寻找速度 有妙招

上距離速度時間 ニスヌーピー壁紙

如何计算速度 有妙招

Ppt 行政职业能力倾向测试powerpoint Presentation Free Download Id 599

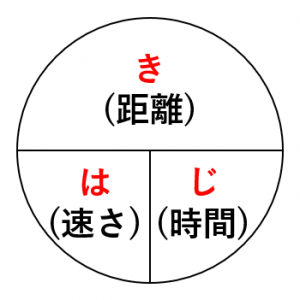
速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学

怎么计算初速度 生活百科

4种方法来求出速度

例題 速率的三個公式應用3 時間 距離 速率 數學 均一教育平台

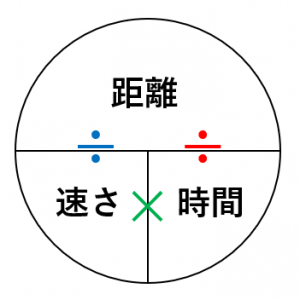
速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学

加速度運動

路程速度时间公式一般用v表示常见单位有米 秒

大嘴鳥親子雜誌

如何计算光年 社会 October 21

如何找到速度公式 自然科学21

兩種思路 解決數學裏的時鐘問題 每日頭條

考虑空气阻力的自由落体 下落的时间和的公式是什么 球体自由落体空气阻力公式 人社网

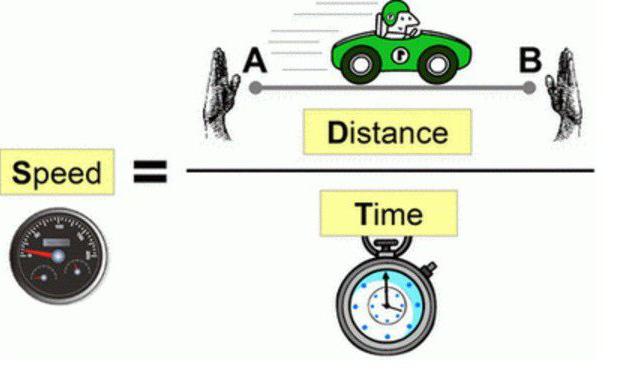
的公式 速度 时间 距离 如何解决这个问题呢

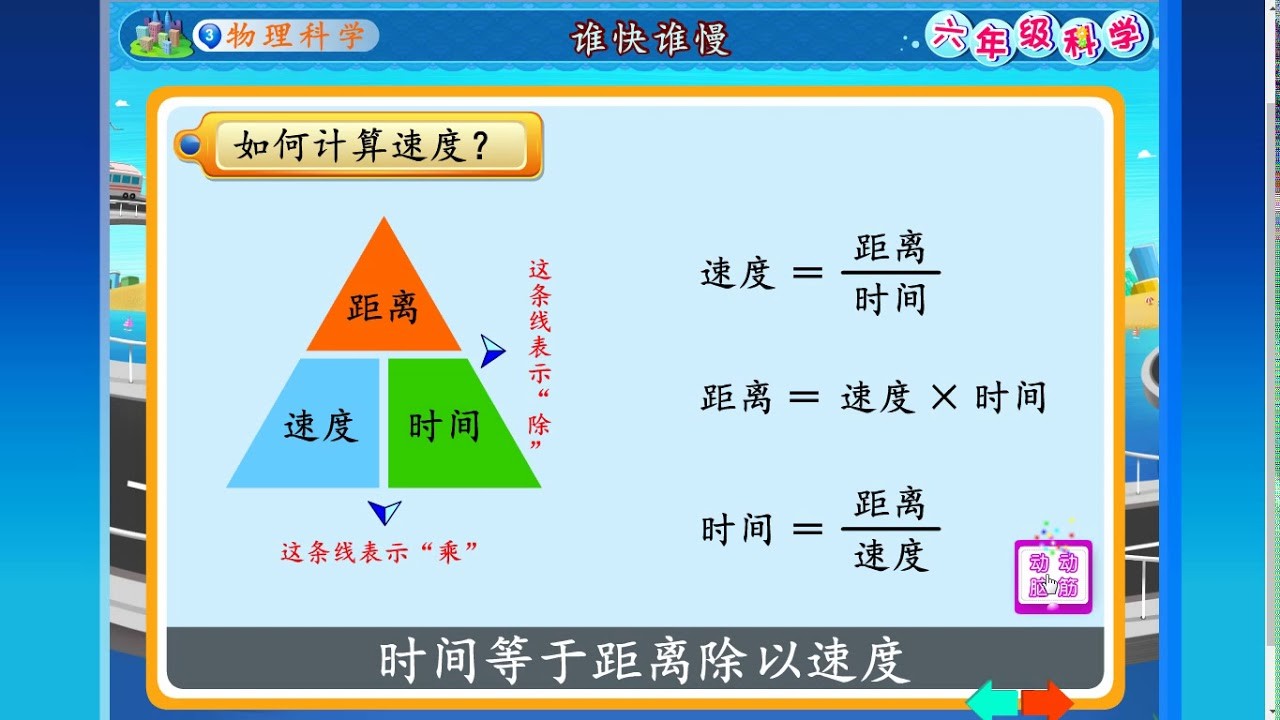
六年级科学速度 Science Quiz Quizizz

为什么当速度趋于光速时 无论多远的距离 都能瞬间到达 全网搜

問題探討 愛因斯坦的相對論的確錯了

一种适用于fmcw汽车雷达目标速度扩展方法与流程

時速公式時間 距離 速度 Cforf

行程赶路一会快一会慢 用等距平均速度公式秒解答案

最新のhd距離速度計算 最高のカラーリングのアイデア

展讯 费利佩 潘通 距离 速度 时间 公式 摩登氧分

如何寻找速度 有妙招

在物理中求时间速度距离的公式用字母怎么表示 物理距离公式 二安网

上距離速度時間 ニスヌーピー壁紙

路程速度时间公式一般用v表示常见单位有米 秒

太阳2 为什么当速度趋于光速时 无论多远都能瞬间到达 地球

3种方法来计算初速度

方程解决问题的公式 西瓜视频搜索

路程的远近 速度的快慢 时间的多久之间关系的问题称为行程问题 哔哩哔哩

物理 19届一轮复习人教版匀变速直线运动的规律学案 江苏专用

力学2 加速度 距离与积分 物理速度加速度积分 热啊网

速率 11 速率的三大計算公式 Youtube

加速度公式距离加速度时间距离计算公式 尚书坊

最新のhd距離速度計算 最高のカラーリングのアイデア

小學最全數學公式 趁著暑假有空 讓孩子每天記 Kks資訊網

程小奔编程机器人编程 用程序测量距离 Makeblock