三角形 合同条件 証明 268055-三角形 合同条件 証明

FdData 中間期末：中学数学2 年：合同証明 図形の合同・三角形の合同条件／仮定と結論，逆，反例／合同条件の利用／共通な辺に注目 共通な角に注目／対頂角に注目／平行線に注目／その他／FdData中間期末製品版のご案内 FdData 中間期末ホームページ三角形の相似条件 3組の辺の比 がそれぞれ等しい 2組の辺の比 と その間の角 がそれぞれ等しい 2組の角 がそれぞれ等しい 合同条件と似ているのがわかるかと思います。 1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」が動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

パターンの暗記で楽勝 三角形の合同の証明のやり方

三角形 合同条件 証明

三角形 合同条件 証明-中学数学教科書「未来へひろがる数学」Q&A 三角形の合同条件の記述が，以前の教科書と変わっていますが，その理由を教えてください。 三角形の合同条件の記述 (2年p96)について，平成24年度教科書から次のように変更しております。 旧教科書 （1三角形の合同の証明① 下の図で，ab=ac，−bad=−cad である。このとき，¼abd×¼acd で あることを右のように証明した。下線部 をうめて，証明を完成させなさい。 三角形の合同の証明② 下の図で，am=cm，bm=dm であ る。このとき，ab=cd であることを右

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

証明 (合同・相似)が苦手な人へ 教遊者 IC Channel 192K subscribers Subscribe 中2,中3,受験生平行と合同,三角形と四角形,相似「証明 (合同・相似)が苦手な人へ90％以上の証明に使えるテンプレートと素材まとめ」デジタル板書データ Watch later 今回は中学校で習う三角形の合同条件について考えていきます。 目次三角形の合同条件の表現の仕方は？三角形の合同条件の証明は？三角形の合同条件ってなぜこの3つなの？まとめ 三角形の合同条件の表現の仕方は？ 早速合同条件3つを重なりのある二つの三角形の証明を考える場面で，合同な図形の性質や三角形の合同条件に着目し，友とカードを順序良く並べ，証明の方針を説明する。 13 前時の自分の証明を振り返り，よい証明と比較しながら，正確に証明をつくる。 14・15

証明の手順 1．仮定を探して書く ↓ 2． 仮定以外 で同じ大きさのものを書く ↓ 3． 「三角形の合同条件」 の3つのうち、どれかを書く ↓ 4．結論を書く証明はこの手順で進めるものです。 "2と3の部分" で、 苦戦する中学生が多いですね。 ここで三角形の合同条件を思い出して！ 忘れた人はココ：三角形の合同条件 すると、 2組の辺とその間の角がそれぞれ等しい ので、 ade≡ acbとなる。 合同な図形では、対応する辺の長さが等しいので bc=edである。 ・・・（ここまでが答え）三角形の合同の証明（応用）中2数学 え、1日27円のプロ家庭教師!？ 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・証明の手順に慣れよう ・等しい角の表し方に慣れよう 完璧じゃなかっ

三角形は三角形に等しく、 残りの2角は残りの2角に、 すなわち 等しい辺が対する角は それぞれ等しい であろう。 いわゆる二辺挟角相等の合同条件である。 三角形は定義1ー19の補足2による。 辺は定義1ー19の補足による。数学・算数 三角形の合同・相似条件についての質問です。 三角形の合同条件と相似条件についてです。 合同条件で二つの三角形が合同になることを中学生に分かるように教えたいのですが、うまい証明法があれ 質問No三角形の合同条件証明のときに絶対にしておかないといけない 中学2年生の数学証明①三角形の合同条件と証明の書き方 塾 内接する四角形に関する証明問題 数学高校に関する質問 中2数学正三角形の証明練習編 映像授業のtry It

Www1 Gifu U Ac Jp Math Gifumathj Pdf

中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材

 三角形の合同証明の練習問題2 練習問題の解答2 ACMと BDMにおいて 仮定より AM＝BM① ①②③より、1組の辺とその両端の角がそれぞれ等しいので 合同な図形では、対応する辺の長さは等しいので、AC＝BD 以上が、中2数学の「証明」しくみ・流れから代表問題 を勉強してきたよね。 両方とも 数学の証明 のために必要なアイテムだから、テスト前には覚えなきゃいけないね。 念のためおさらいしておくと、 三角形の合同条件 3つの辺の長さがそれぞれ等しい 2組の辺の長さとその間の角が等しい 両端の角とその間の辺の長さがそれぞれ等しい 三角形の相似条件 3組の辺の比がすべて等しい辺が等しいことを明らかにするためには、図形の中からその辺をふくむ合同な三角形を見いだ し、三角形の合同条件を用いて演繹的に説明すればよいことが分かる。 (2)シミュレーションソフト活用の意図と方法 ① 『仮定』をクリックすれば，仮定となる辺 が点滅し，『着目する三角形』をクリックすれ ば，証明したい2つの三角形が点滅する。こ の操作で，図の中

パターンの暗記で楽勝 三角形の合同の証明のやり方

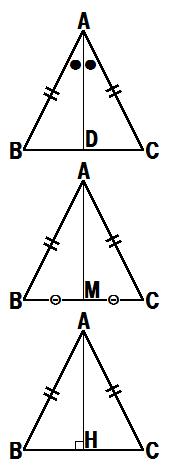
三角形の合同条件と二等辺三角形の底角 2 算数 数学記事

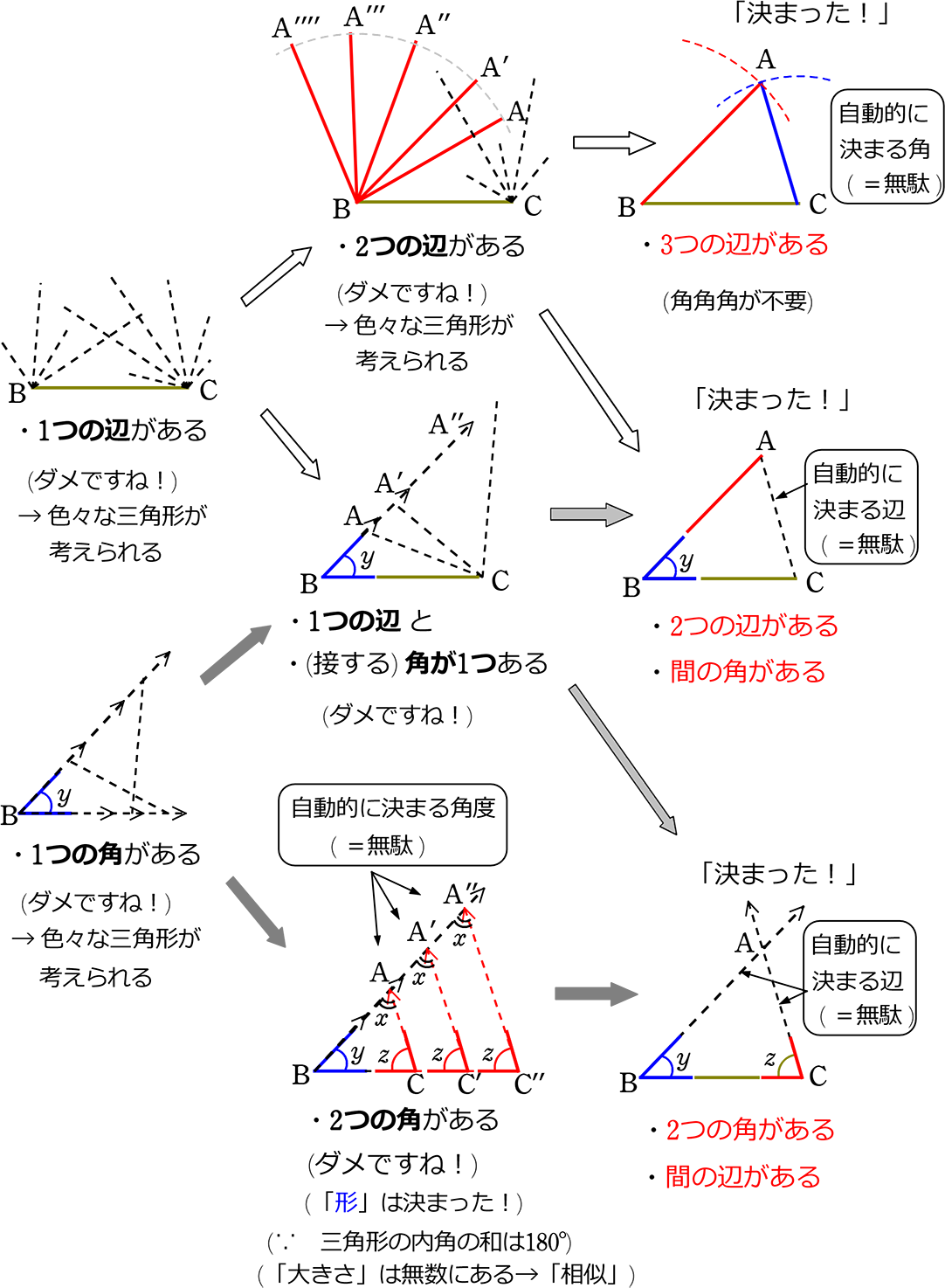
 三角形の合同条件を使って、合同な三角形を見つける方法！ 証明の書き方合同な三角形の証明問題の書き方を基礎から解説！←今回の記事 直角三角形証明問題の書き方とは？合同条件の使い方を徹底解説！ 二等辺三角形の角度の求め方 厳選6問解説！仮定と結論，逆，合同条件／三角形の合同の証明／二等辺三角形の定理／ 二等辺三角形の性質を使った証明 ／二等辺三角形になることを証明／正三角形／ 直角三角形／ 平行四辺形の性質／平行四辺形になるための条件／長方形・ひし形・正方形／ 折り返し授業実践 (1) 実践内容 「三角形の合同」 （本時は2時間扱い中の第1時） （生徒数40人で2人のティームティーチングによる授業） (2) 本時のねらい 1) 三角形が1通りに決まる場合を見つけ，合同条件と結びつけることができる。 三角形が1通りに決まるか

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ

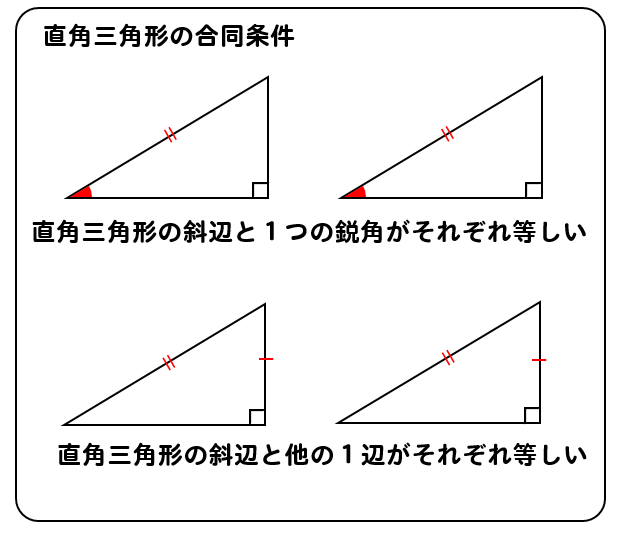
直角三角形の合同条件 直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき（証明） 2 斜辺と他の1辺が、それぞれ等しいとき（証明） 三角形の成立条件とその証明 レベル ★ 基礎 平面図形 更新日時 三角形の成立条件（存在条件）：三辺の長さが a, b, c a,\b,\c a, b, c である三角形が存在する必要十分条件は， a b > c ab > c a b > c かつ 証明してみた 中学数学では三角形の3つの合同条件というものを習いますよね。 しかし、習った当時はひたすらに覚えろと言われ、理解せずにただ覚えた人が大半なのではないでしょうか。 そこで今回は、改めて三角形の合同条件について考えてみようと思います。 中学校はとっくの昔に卒業した大人の方でも、数学好きの中学生の方でもわかるように

直角三角形の合同条件とそれを利用した証明 チーム エン

2 の直角三角形の合同条件は何ですか 理由も付けて教えて頂けると助かります Clear

適切な三角形の合同条件を用いて，三角形の合同を証明する。このことから， 予想される性質がいつでも常に成り立っていることを，論理的に明らかにす る方法を理解する。 活動の流れ 数学的な考え方 学習活動 3 演繹的に推論する直角三角形の合同条件を用いて，証明しよ用いて，積極的に証明しよ用いて，証明しようとする。 うとする。 うとする。 （観察・ワークシート） 数学的な見方や考え方 直角三角形の合同条件を 直角三角形の合同条件を 直角三角形の合同条件を用いて，図形の性用いて，図形の性質の証明用いて，図形の性質の証明 三角形の合同証明の総合的な練習問題です。定期テスト対策や高校入試対策としてもご利用ください。三角形の合同証明のポイント基本的な合同条件、証明のやり方をしっかり確認してから取り組んでください。 三角形の合同 二等辺三角形 直角三角形1合同なることを証明する三角形を囲ん

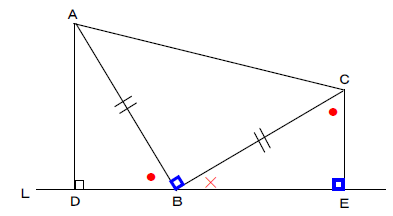
中2数学 直角三角形の合同証明のポイントと練習問題 Atstudier

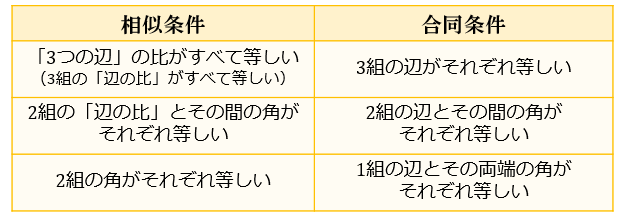
三角形の合同条件 相似条件と合同条件の違いとは アタリマエ

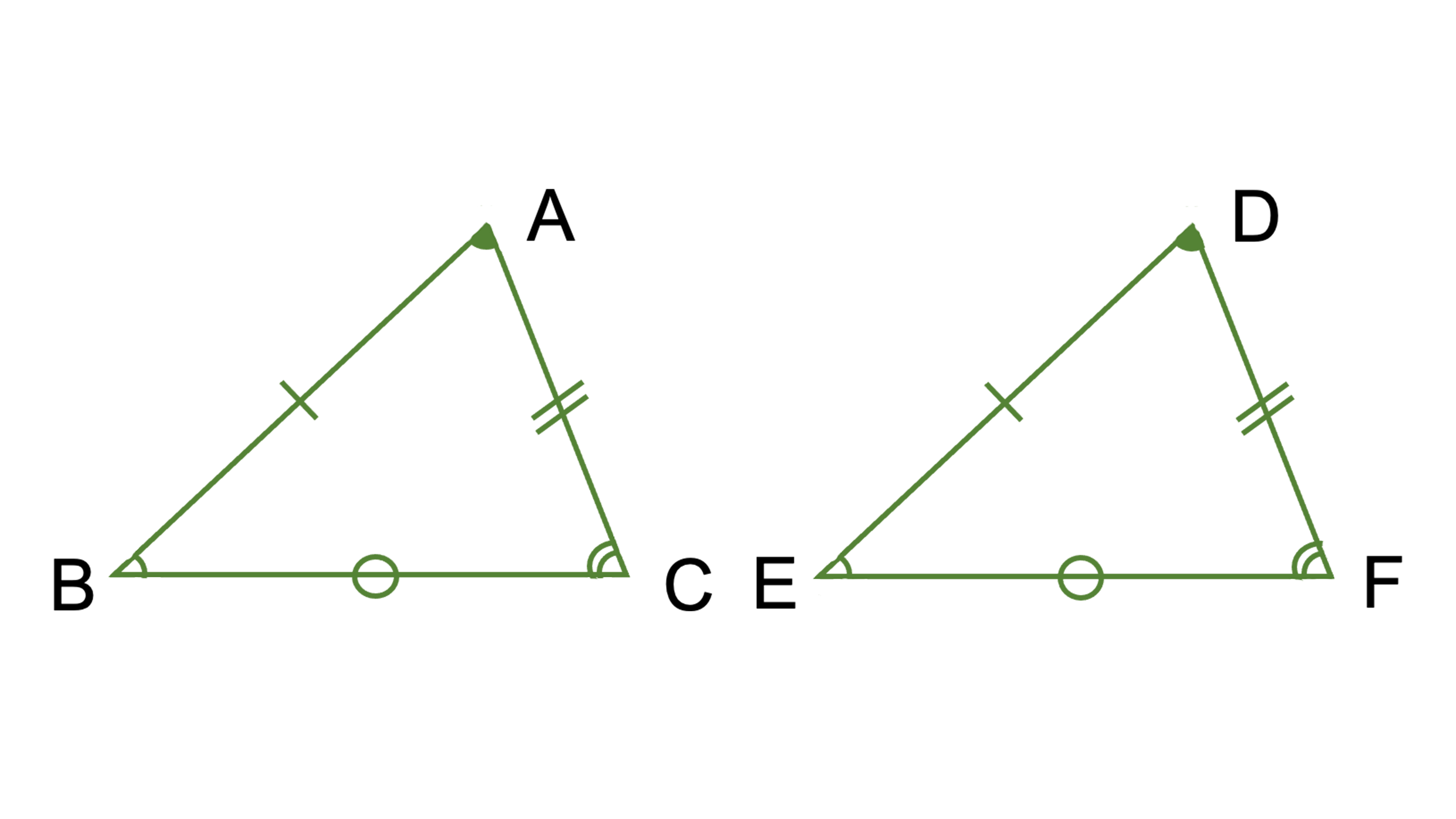
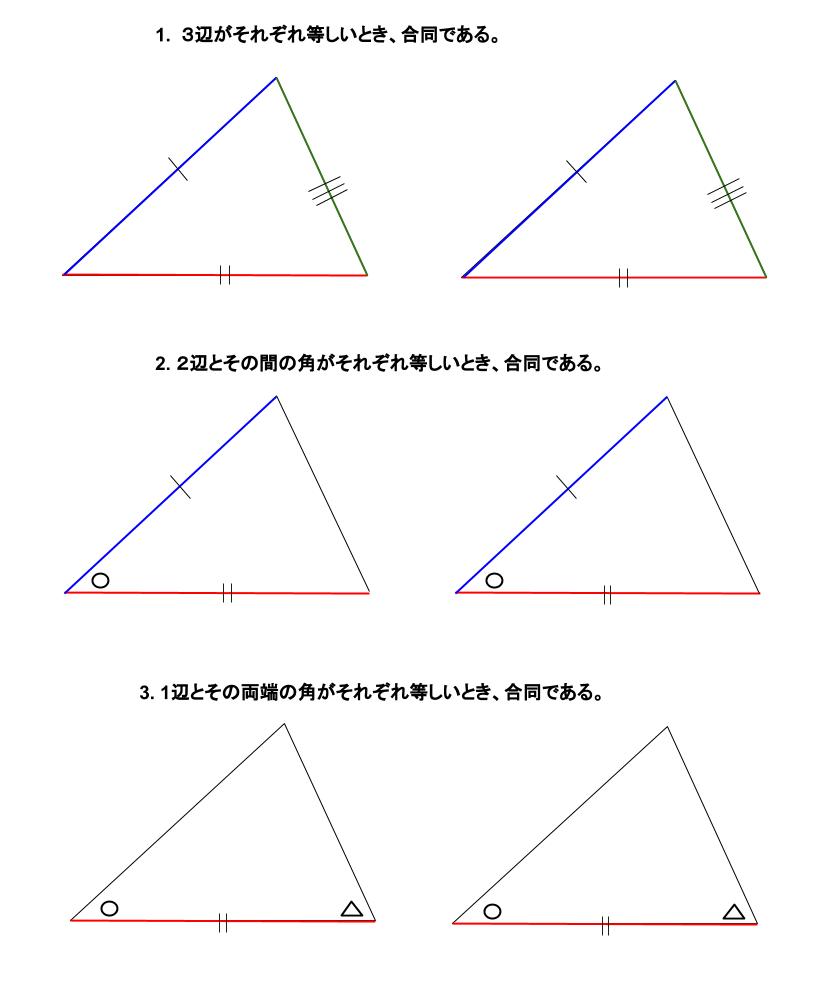
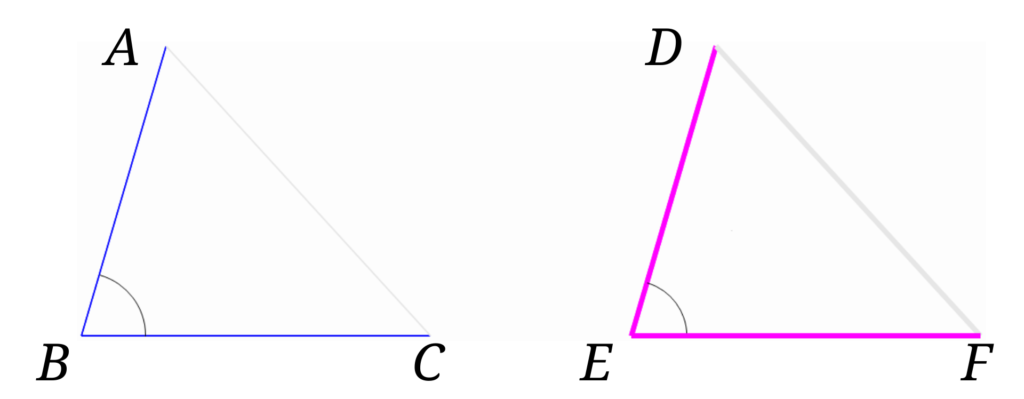
直角三角形の合同条件が使えるのは 斜辺が等しいことが分かっているときだけ なので注意しておきましょう！ 直角三角形の合同証明の書き方とは 直角三角形の合同条件を利用した、合同証明の問題に挑戦してみましょう。 二等辺三角形の形 2つの三角形を ABCと DEFとします。 二辺夾角相等 AB＝DE，AC＝DF，∠A＝∠Dだとします。 ∠Aと∠Dが重なるように移動させると，半直線ABと半直線DE，半直線ACと半直線DFが重なります。 そしてAB＝DE，AC＝DFより頂点Bと頂点D，頂点Cと頂点Fが重なることになります。 よって ABCと DEFは合同です。 二角夾辺相等 BC＝EF，∠B＝∠E，∠C＝∠Fだとします。 辺BCと辺EFが 3つある三角形の合同条件とは 合同な三角形同士には一定の条件が3つ当てはまります。 決まり文句としてそのまま書くようにしてください。 3組の辺がそれぞれ等しい ※上の三角形ABCと三角形DEFでいえばAB=DE、BC=EF、CA=FD 2組の辺とその間の角がそれぞれ等しい ※上の三角形ABCと三角形DEFでいえばAB=DE、BC=EF、∠ABC=∠DEF 1組の辺とその両端の角がそれぞれ

Www1 Gifu U Ac Jp Math Gifumathj Pdf

中２数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾

 第1巻命題4 三角形の合同条件（二辺夾角相等） 第1巻 第1巻命題 第1巻命題命題104 公理7 公理9 もし二つの三角形が二辺が二辺にそれぞれ等しく、その等しい二辺に挟まれる角が等しいならば、底辺は底辺に等しく、三角形は三角形に等しく、残りの二角三角形の合同を証明する 三角形の合同条件をそろえることで証明できる 例1 cはadの中点で, ∠bac=∠edcのとき bac≡ edcとなることを証明。 a b c d e 対頂角 仮定を図に描きいれる。 >>仮定 これだけでは合同条件がそろわないので、 理由があって 等しくなる角や辺を探す。

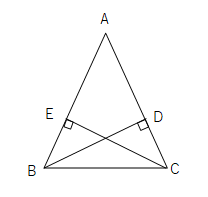
中2数学 直角三角形の合同証明のポイントと練習問題 Examee

三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

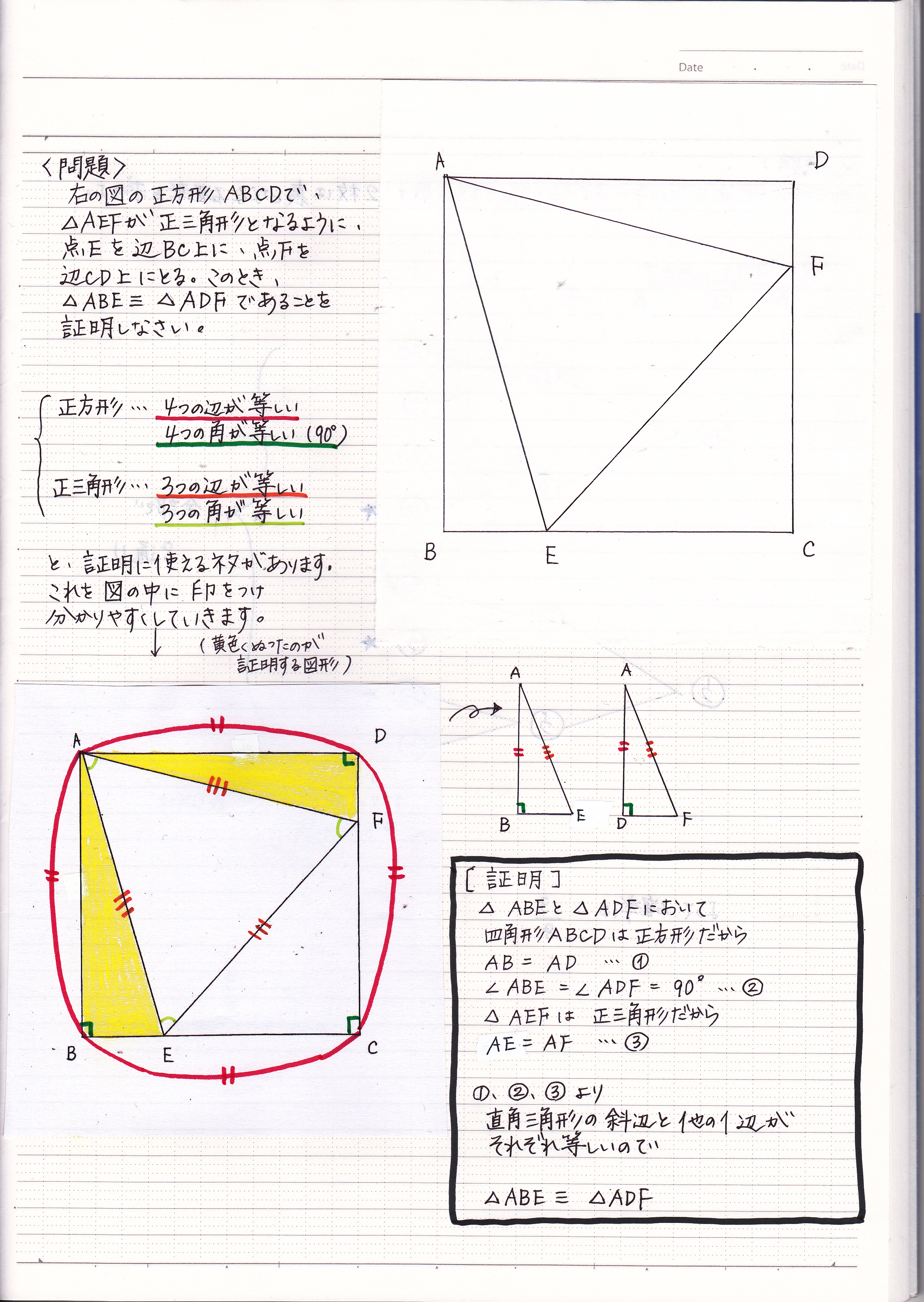
直角三角形の合同条件を使った証明問題の解き方 2 現役塾講師のわかりやすい中学数学の解き方

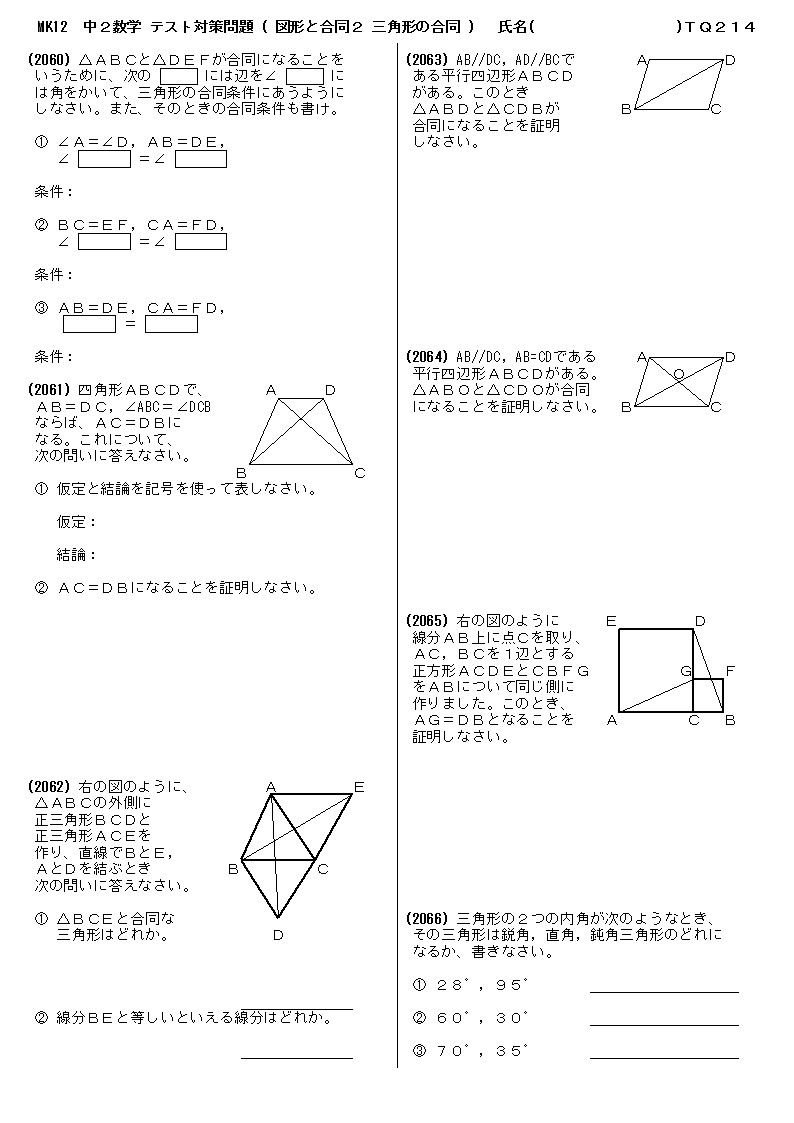
無料 中２数学 テスト対策 問題プリント 214 図形と合同２ 三角形の合同

三角形の合同証明の練習 無料で使える中学学習プリント

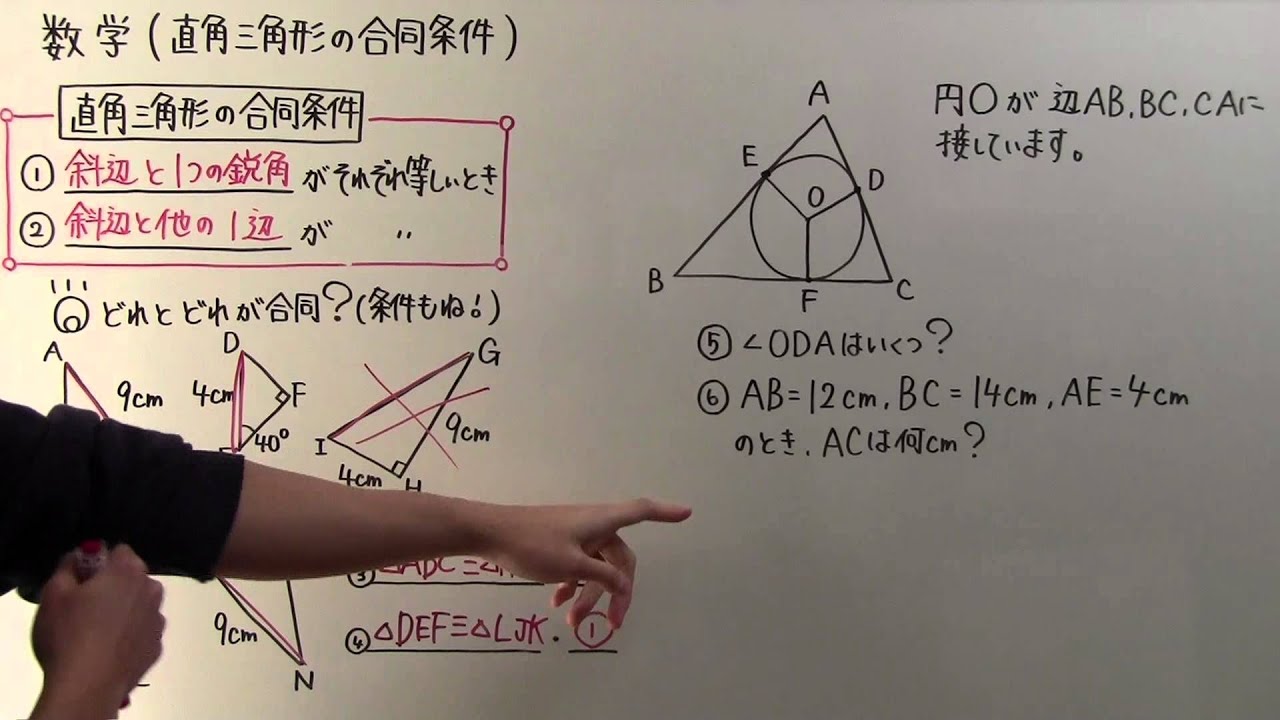
中学2年の数学 動画 直角三角形の合同条件の問題 19ch

数学 中学2年 三角形 1 合同 Youtube

二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角形と四角形 三角形の合同の証明のしかた 中学数学 定期テスト対策サイト

三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

三角形の合同条件

中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく

三角形の合同条件 小学生 中学生の勉強

三角形全等的条件 你会几种 5种常用三角形全等辅助线添加方法 有5道例题详解 个税扣除的条件 成人高考的条件 取保侯审的条件 一点通指南网

世界一わかりやすい数学問題集中２ ４章 平行と合同と証明

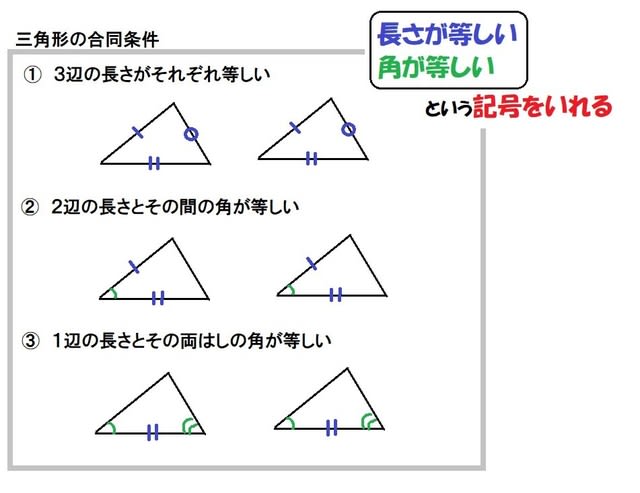
合同な図形 小５ 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support

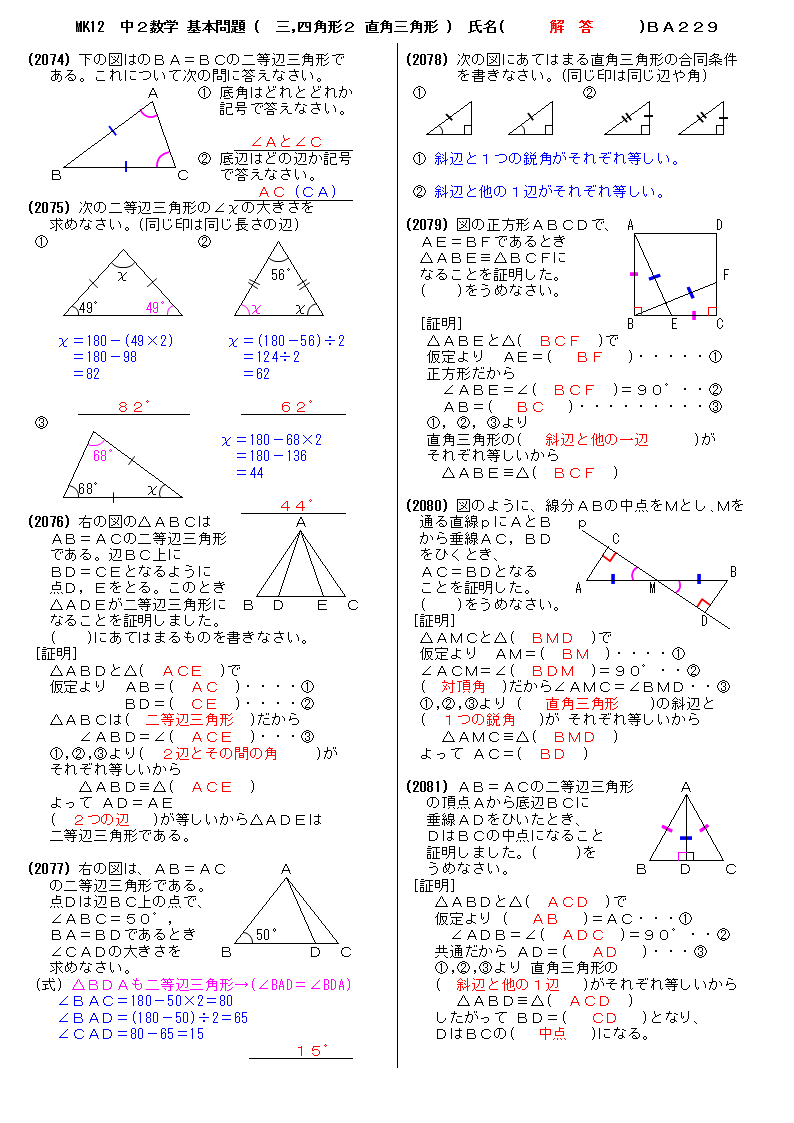
無料 中２数学 基本問題 解答プリント 229 三角形 四角形２ 直角三角形

中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su

直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ

合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典

中学数学より３ 三角形の合同条件 身勝手な主張

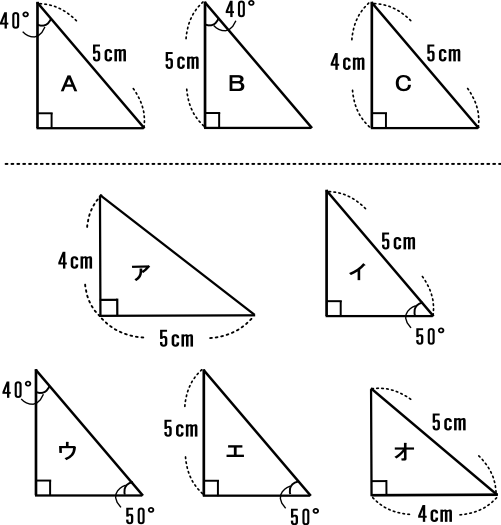
中学２年数学練習問題 直角三角形の合同条件と証明問題 図形と合同

中学数学 図形の合同 図形の性質

Studydoctor三角形の合同条件 中２数学 Studydoctor

直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学

3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ

直角三角形の合同条件

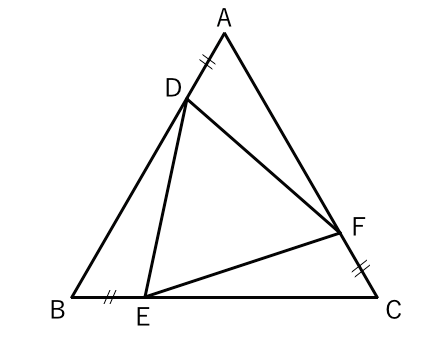
合同な図形 正三角形の証明問題 苦手な数学を簡単に

上数学合同条件 ニスヌーピー壁紙

三角形の合同条件

直角三角形の合同の証明の問題です わからないので教えてください お願いします Clear

中学数学 図形の合同 図形の性質

直角三角形の合同条件とその証明 数学fun

三角形の合同証明の練習 無料で使える中学学習プリント

直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ

数学 中2 56 三角形の合同 基本編 Youtube

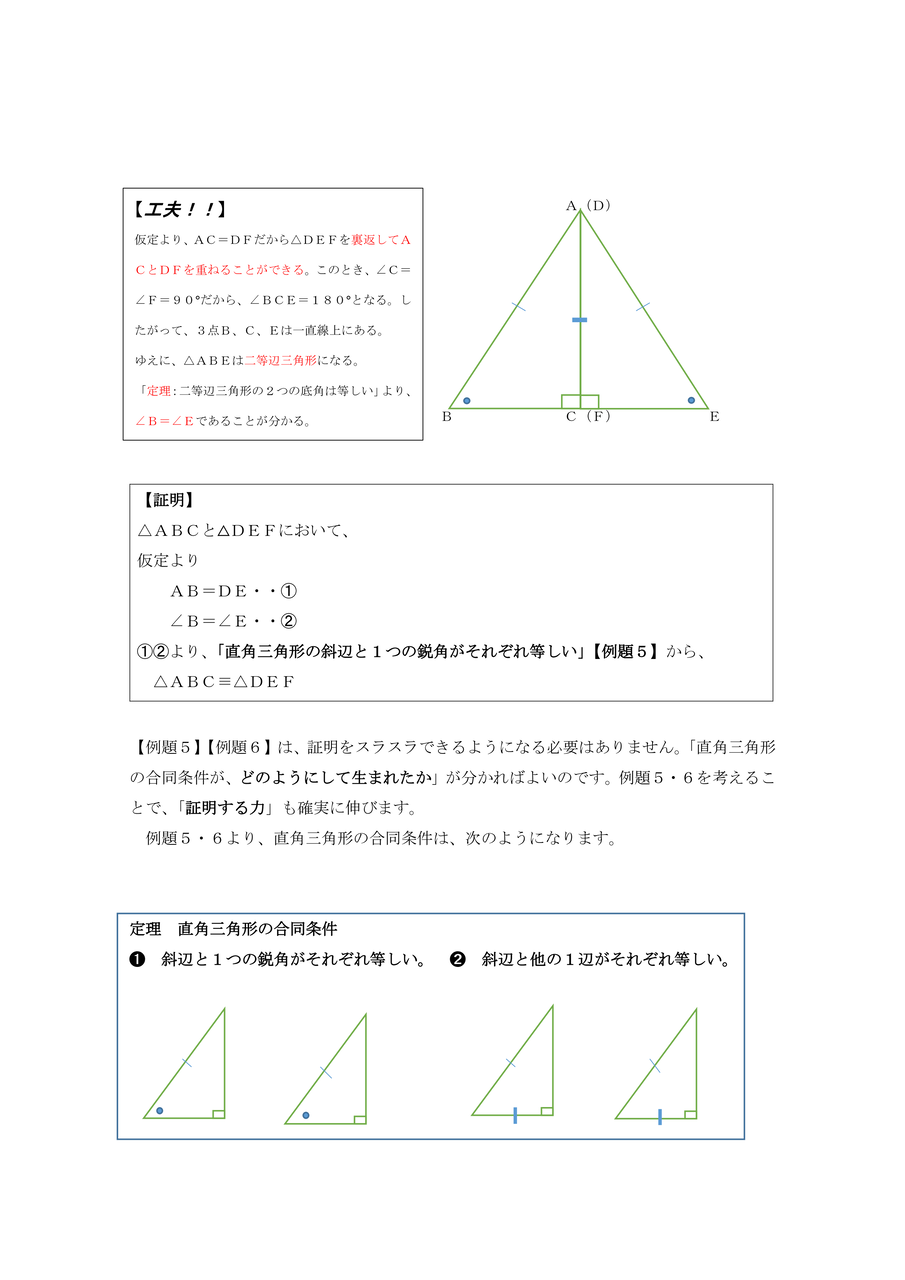
中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材

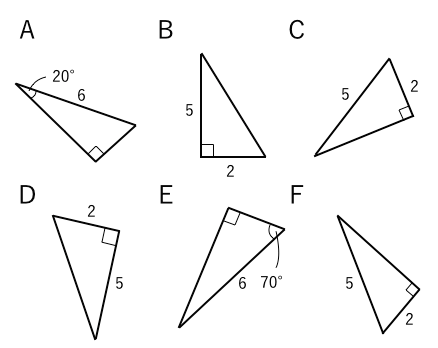
直角三角形の合同 証明問題 苦手な数学を簡単に

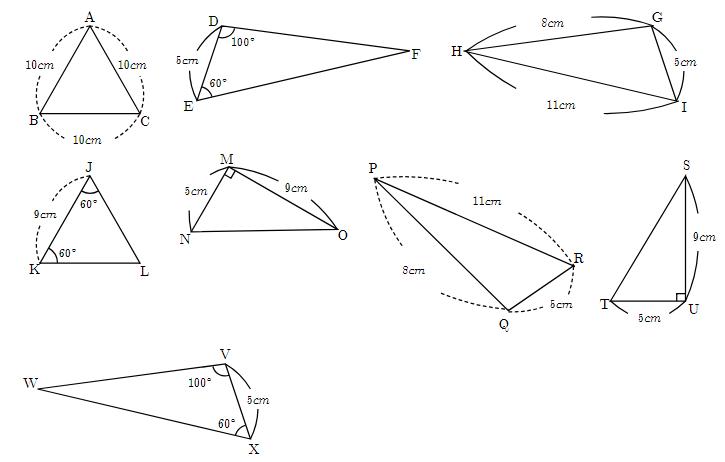
中2数学 三角形の証明の仕方 Pikuu

最も人気のある 三角形合同証明 ニスヌーピー壁紙

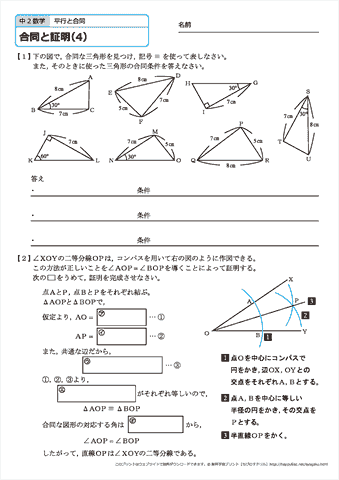
中学２年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

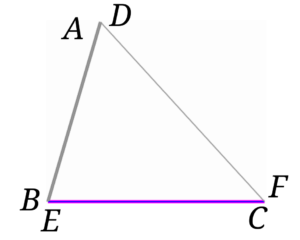
三角形の合同条件の表現ってなぜこの3つなの まぜこぜ情報局

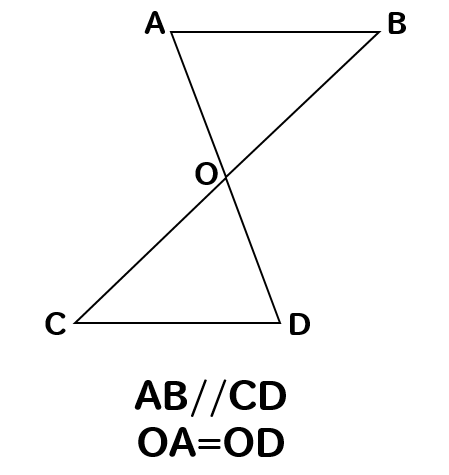
三角形の合同条件 合同な図形の見つけ方 証明問題の基礎を身につけよう 数スタ

三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学

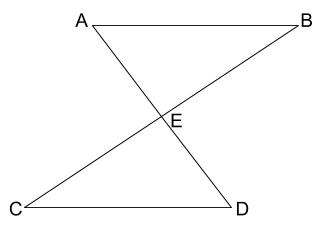
中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su

中２数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン

三角形の合同条件を使った証明問題 中学２年生の問題を解こう 身勝手な主張

合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典

Studydoctor三角形の合同証明の進め方 中２数学 Studydoctor

本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download

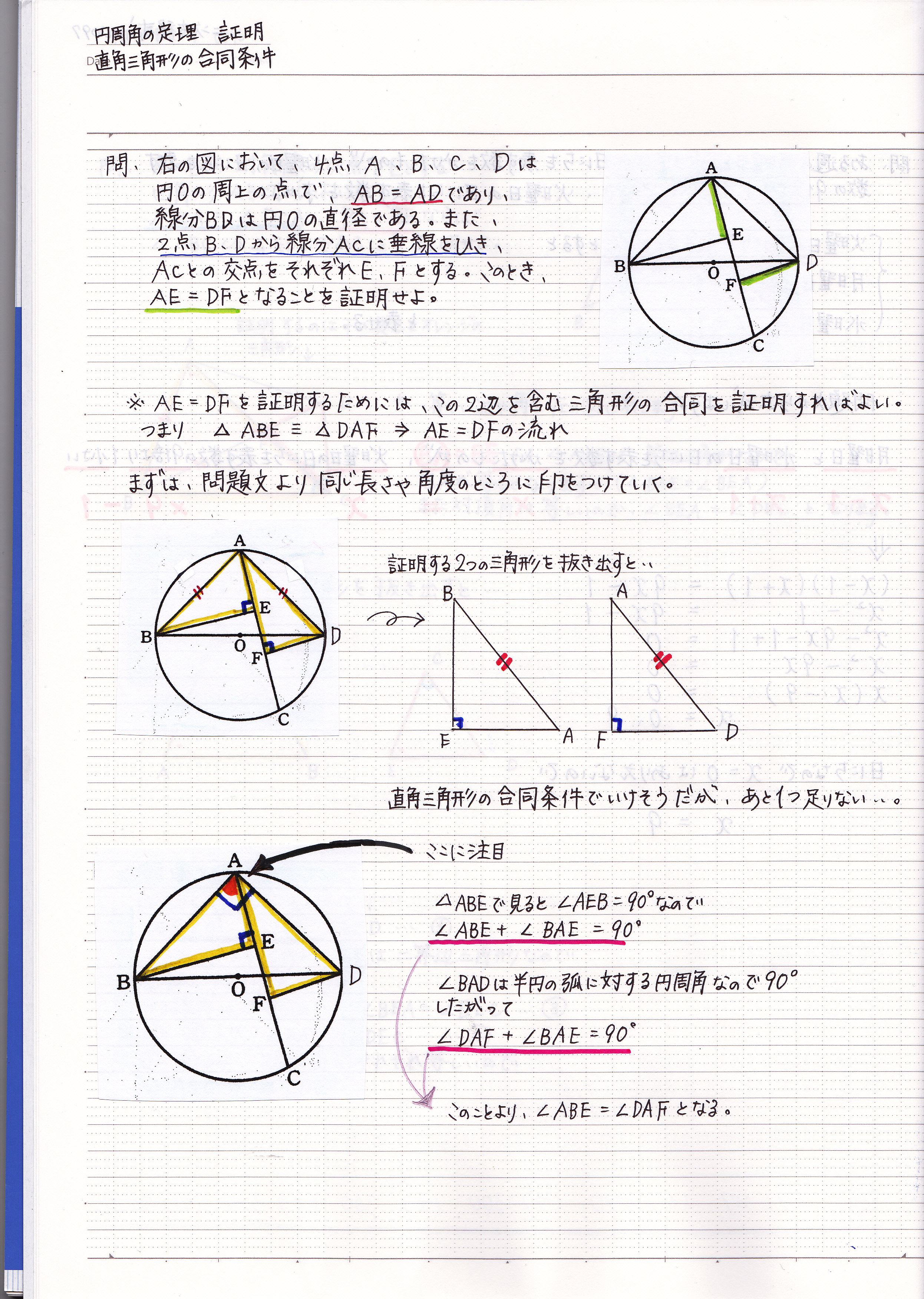
直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方

合同と証明 Ict教材eboard イーボード

三角形の合同条件の表現ってなぜこの3つなの まぜこぜ情報局

A Lihat Cara Penyelesaian Di Qanda

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

三角形の合同条件 相似条件と合同条件の違いとは アタリマエ

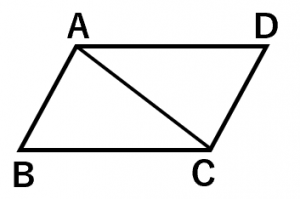
三角形の合同条件を図で分かりやすく説明 具体例で学ぶ数学

直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題

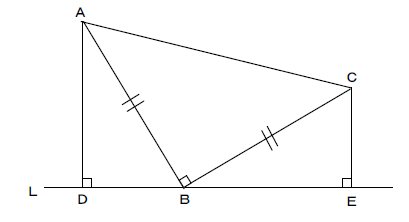
中2数学 直角三角形の合同証明のポイントと練習問題 Atstudier

合同と証明 Ict教材eboard イーボード

U9j580gf8iba369ji2w Xyz P 970

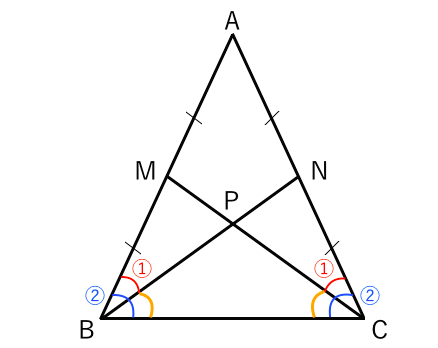
合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に

保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく

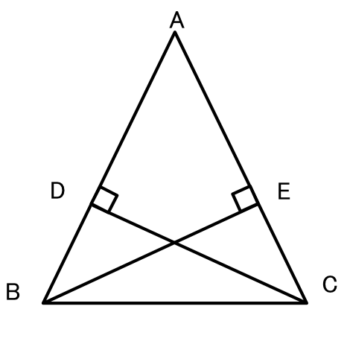
フロー 2 5 4 4 直角三角形の合同条件を利用した証明

三角形の合同条件 証明のときに絶対にしておかないといけない問題 中学や高校の数学の計算問題

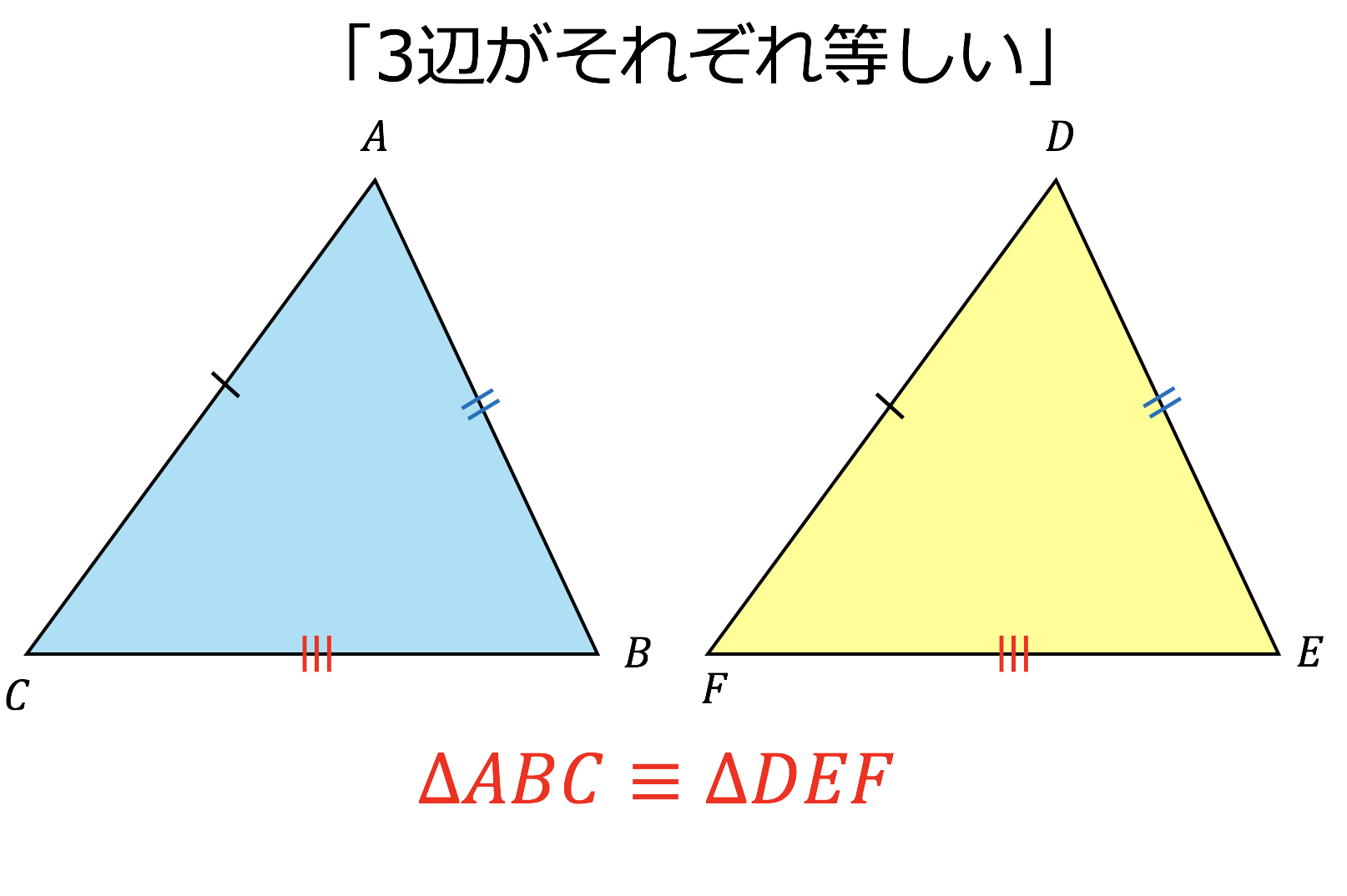
3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ

三角形の合同条件 板書

三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学

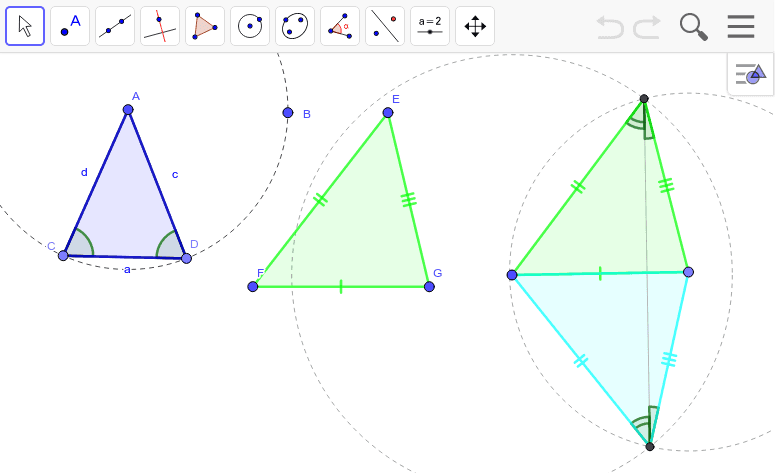
三角形の合同条件３辺 Geogebra

合同ということを証明してください直角三角形の合同条件を使わずに Yahoo 知恵袋

國二junior High数学的証明 中二 筆記 Clear

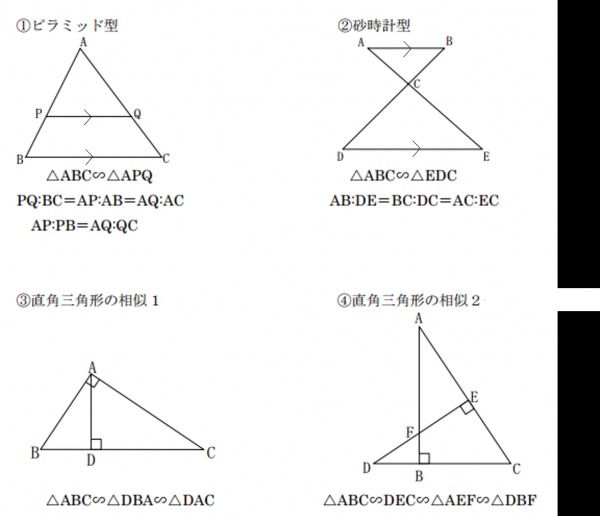
三角形の相似 合同条件 優技録

三角形の合同条件と証明問題の解き方 数学fun

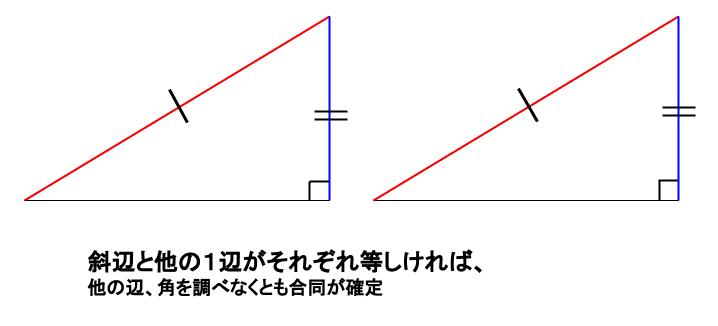
中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su

最も人気のある 三角形合同証明 ニスヌーピー壁紙

中2数学 三角形の合同を証明する問題 練習編 映像授業のtry It トライイット

中2数学 三角形の合同条件２ ２辺とその間の角 練習編 映像授業のtry It トライイット

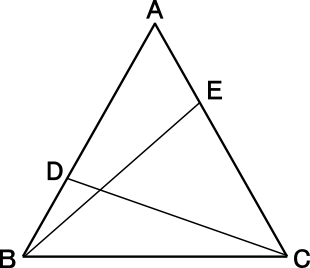
中学２年数学練習問題 図形の合同条件と証明の進め方の解答

三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学

直角三角形の合同条件再び 中学校２年生の数学 身勝手な主張

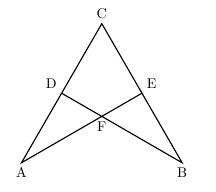
三角形の合同の問題の解法 夢を叶える塾

Aebc Adae E Descubre Como Resolverlo En Qanda

中２数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト

中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋

直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方

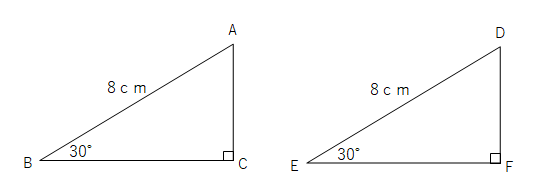
中2数学 直角三角形の合同証明のポイントと練習問題 Examee

三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学

直角三角形の合同条件とその証明 数学fun

Incoming Term: 三角形 合同条件 証明, 三角形 合同条件 証明 問題,