√画像をダウンロード 三 連立 方程式 313088-三連立方程式 サイト
三次方程式の解を出すプログラムを作成するために、出力データの確認として使用させていただきました。 とても便利です。 4 1723 歳代 / 高校・専門・大学生・大学院生 / 役に立たな次の連立方程式を解け。 4 5 x 31 15 y5 2 = 13 10 06x08y=16 4(2xy3)(5x3y)=6 022x032y=104 3(3x2y)=8(2xy) x 3 1 2 = x2 6 y 3 8x5 311y7 12 =11 4 5x7 39 4 y=8 次の問いに答えよ。 次の連立方程式を解け 2(3x8y)7x2y=3(2x4y3)2=4(5x9y)10 連立方程式 7xay=2a 11x9y=12 の解の比が x y = 3 4のとき、aの値を求めよ。04連立方程式の解き方 連立方程式とは?方程式の解中2数学 連立方程式の解き方(加減法①)中2数学 連立方程式の解き方(加減法②)中2数学 連立方程式の解き方(代入法)中2数学 05いろいろな連立方程式 かっこのついた連立方程式

單元8 三元一次聯立方程式p160 1隨堂練習動態解題 Youtube
三連立方程式 サイト
三連立方程式 サイト-Excelを用いた連立方程式の解法 このページでは,Excel関数を使って連立方程式を解く手順について解説する. 手順 連立方程式を行列で表現し,行列Aと行列Cの係数をExcelシートに入力する.抵抗に関する連立方程式を解く必要がある。そこで,「キルヒホッフの法則」を説明する前に,ここ では数学的な準備として,未知数が二つの2 元連立1 次方程式と変数が三つの3 元連立1 次方程式に ついて,クラーメルの公式による解法を説明する。 1



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf
連立方程式と考えると は,未知数が3個,方程式が2個だから不定解になる.そこで,どれか1文字,例えばzについては解かないことに決めて,x, yをzで表す.かっこ( )内の文字については解かない.一次の連立漸化式の解き方を3通り解説します。 a n a_n a n , b n b_n b n のいずれか片方を消去することで,三項間漸化式に帰着させます。自分は高校時代,この解法を使っていました。 この連立方程式6x14y7x=27 6x14y7x=27を 整理してx14y=27 x14y=27の両辺に3をかけ、辺々たすと 3x10y = 23 ) 3x42y = 81 52y = 104 両辺を52で割るとy=2 y=2を3x10y=23に代入すると 3x=23 3x=3 x=1
連立方程式 例題 連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつくAx =LU x= b x=A−1b =U −1L−1b A x = L U x = b x = A − 1 b = U − 1 L − 1 b お客様の声 アンケート投稿 よくある質問 リンク方法 「三数の内の二数の和」→ 和差算とその派生問題 「三数の内の二数の積」→ 和差算の派生問題(追加) 又、定数a,b,cは全て正の数であるとします。 問題1 本記事で考える問題の一つ目は以下の通りです。問題の種別としては三元二次連立方程式となります。
連立 1 次方程式に基本変形をして得られた方程式と元の方程式とは等価な方程式である. すなわち両者は同じ解をもつ. 連立 1 次方程式とその行列表現は,方程式としては等価なものである. 連立 1 次方程式の基本変形は,行列表現では次の行列の行の基本変形となる. 定義 39(行列の行の基本変形) 行列に対する次の操作を行列の行の基本変形(matrix elementary row連立線形微分方程式 {x ′ = ax by y ′ = cx dy について いずれか一方の関数の線形2階斉次微分方程式に帰着させて解くことができるようになります。 微分演算子を用いた表現により,連立方程式を解くことができるようになります。 係数行列の対角化に最後にもとめたもの以外には、最初の連立方程式の解はないのでしょうか。そういうこと も考えていきたいと思います。 33 既約ガウス行列と基本定理 n 変数の1次方程式m 個からなる連立一次方程式は、 8 >> < >> a11x1 a12x2 ···a1nxn = b1 a21x1 a22x2 ···a



Http Blog Ncue Edu Tw Sys Lib Read Attach Php Id




Matlab方程式求解 Ytffhew的博客 程序员宅基地 Matlab方程式求解 程序员宅基地
連立方程式の同値変形について 27について質問です。 ①かつ②→③かつ④ は成立していると分かりますが、 ①かつ②←③かつ④ この成立を示さなければ解答として不充分ではないのでしょう 連立方程式の解き方基本:加減法 加減法とは、わかりやすくいえば ステップ1:複数の方程式が共通して持つ文字の中から1つの文字を選び、その文字の係数をそろえる ステップ2:係数をそろえた文字が消去できるように、方程式を足したり引いたりする三元連立方程式 110 /14件 表示件数 5 10 30 50 100 0 1 0008 女 / 歳未満 / 高校・専門・大学生・大学院生 / 役に立った / 使用目的 検算 ご意見・ご感想 自分の計算が不安で利用させていただきました。



二元一次聯立方程式的解 Live 多媒體數學觀念典online



Http Math Ymhs Tyc Edu Tw Chenjt99 Scrclass 1052 E9 Ab 98 E4 Ba 8c E9 Ab 98 E4 Ba 8c E7 Bf 92 E9 A1 8c 2 3 E7 Bf 92 E9 A1 8c Pdf
単 元 連立方程式 中国の数学 1単元のねらい 変数が1つの一元一次方程式ほ第1学年で指導しておれ ここでほ,変数が2つの二元一次 方程式を指導する。 連立方程式の解法に習熟させることが一番のねらいであるが,技能面だけに重点を置くので第三回連立方程式の解法 ガウスの消去法・行列 舟木剛 平成24年10月24日2限 数値解析‐3 1 シラバス • 授業の目的 – 工学分野でよく用いられる数値計算の算法ならびにそれらの数値的な特性について理解させる. • 授業計画 – 数値計算と誤差(1回)動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




數學不好的人所欠缺的解題基本功 圖表與聯立方程式之間的聯繫 每日頭條



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf
連立1次方程式の解法まとめ 「定常」反復法(Jacobi, GaussSeidel, SOR) 使用制限: 対角優位(第i行の対角項の絶対値がそれ以外の成分の絶対値の和より大きい) 直接法(Gaussの消去法,GaussJordan, LU分解) 使用制限: 対角項がゼロではない。(Pivoting による回避が必要)3x−4y5=2xy−4=5x−3y1 この形の方程式を解くとき,普通の方程式を解くときの 「移項」のような変形をしにくい ので,解き方のコツを覚えておくとよいでしょう. 解き方 〇「 A=B=C 」というのは,「 A=B かつ B=C 」を省略的に書いたものです.だから,「 A=B=C 」という方程式が与えられたら,「 A=B かつ B=C 」に直して解いたらよいのです. A=B=C → A=B 式が3つ並んでいる方程式のときには、それぞれ2つの式を組み合わせて連立方程式を作る。 \(A=B=C\) の方程式のとき $$\begin{eqnarray} \left\{ \begin{array}{l}A=B \\A=C \end{array} \right \end{eqnarray}$$



Http Www Powercam Cc Home Read Attach Php Id 1




建宏國中e把罩數學 3 二元一次聯立方程式
連立方程式の求解 •元数の多い連立方程式の手計算はむずい •連立方程式を計算機で解く •解き方の種類 •直接解法 •反復解法 •代表的な解き方 •ガウスの消去法→直接解法。乗除算回数低減。精度高める。 •ガウス・ジョルダン法 •ヤコビの反復法本稿では,特にNeumann条件が与えられた境界値問題に対する方程式の差分化によって得られる,巡 回型三重対角連立一次方程式を対象とする.対象とする巡回型三重対角連立一次方程式を,次式のように 行列を用いて表す. dl e1 0 c2 d2 e2 0 O c3 d3 e3 O1 変数を方程式の逆の辺に移項します。 この「代入法」は、一つの式で「xを解く」(または他の変数を解く)ことから始まります。 例として、 4x 2y = 8 と 5x 3y = 9 という方程式があるとします。 まず最初の方程式だけを見ます。 両辺から2yを引いて式を変形させると、 4x = 8 2y となります。 この方法ではよく分数を使います。 分数が苦手な場合は、代わりに



March 21 樹洞tree Hole 2 0



Www Boyo Org Tw Boyo Index Php Downloads Category 25 17 10 16 09 09 14 Download 703 Pdf
連立方程式を行列を使って解くことを考えましょう。最初は、未知数が2個の場合 を考えます。以下に、連立方程式を示しました。 上の行列方程式を解いてみます。まず、左から両辺に逆行列をかけます。 ここで、逆行列は以下のように計算されます。連立方程式をより深く考えるための教材 研究の要約 平井安久* 連立方程式の応用問題として課腰解決的な要瀬を含む教材を作成した連立`元一次方担式 を用いる場面から始まり予想外の解が得られる場面,僻のj勘直を推測する場面,一次関数の連立方程式は行列計算を用い解く事ができます。さらにexcelの関数 逆行列を求める関数=minverse と 行列の積=mmultを用いればほんの数秒で解く事ができます。 それでは、以下の連立方程式を実際にexcelで解いてみましょう。



Page 5 Epd307 數學b第三冊學習講義 課本pdf




單元8 三元一次聯立方程式p160 1隨堂練習動態解題 Youtube
定義 38 (連立一次方程式の基本変形) 連立一次方程式に対する次のの操作を 連立一次方程式の基本変形と呼ぶ. (1) 一つの式を 倍する. (2) 二つの式を入れ替える. (3) 一つの式を 倍して別の行に加え式(5)(6)を見て,何かピンと来るでしょうか?式(5)(6)は, と を解とする,次式で表わされる二次方程式の解と係数の関係を表していることに気がつけば,あと一歩です.(この二次方程式を,元の三次方程式の 分解方程式 と呼びます.)連立方程式 (代入法) 連立方程式 (加減法1) 連立方程式 (加減法2) 連立方程式 (かっこのある式) 連立方程式 (A=B=C) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく 文章題速さ 長さのあるもの 文章題 2けたの自然数 文章題 商と余り 文章題 濃度の問題




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf
三項間漸化式の特性方程式の解を α, β \alpha,\beta α, β とおくと,漸化式の一般項は a n = A α n B β n a_{n}=A\alpha^nB\beta^n a n = A α n B β n と表される。 A, B A,B A, B は初期条件から求める。三つの式の連立方程式 About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features © Google LLC連立方程式の解き方を教えてください! 答え4000 (m) A町からB町に向かうときの上りの定 行きにかかった時間について L68 50'80 帰りにかかった時間について = 40'50 の, のを連立方程式として解くと, e=2400, y=1600 連立方程式



1




4 2 3三元一次聯立方程式
中学2年数学 連立方程式 加減法「係数がそろっていないとき」中学校数学習サイト https//math005netcom/reidai/renritu2php練習




二元一次聯立方程式的應用題3 二元一次聯立方程式的應用問題 均一教育平台




單元8 三元一次聯立方程式p161 1隨堂練習動態解題 Youtube



三元一次聯立方程組的解 空間中三平面的關係 中學數學課 隨意窩xuite日誌




加減消去法解二元一次聯立方程式 數學 均一教育平台




基礎 二元一次聯立方程式 數學 均一教育平台



Www Hsinhua Com Tw Wp Content Uploads 6259r E8 95 E9 Ac 86 E5 Ad B8 E6 95 B8 E5 Ad B8c E4 B8 E8 Ac 9b E7 Be E6 95 99 E7 94 A8 Ch4 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E5 8f E8 87 E7 9f E9 99 A3 Pdf



名師課輔網 100學測高斯喬登消去法




使用python 解線性聯立方程組 透過numpy Pyplot 與tensorflow By Yao Jen Kuo Pyradise Medium




二元一次聯立方程式的幾何意義 Live 多媒體數學觀念典online




1 3 2 1 4 2 2 15r




4d F736f F Db2cb3e6a4b8a454a4b8a440a6b8c170a5dfa4e8b57bb2d52e646f63 Pdf 免费下载



三元一次聯立方程式 解三元一次方程組 Youtube



Www Ylvs Chc Edu Tw Ischool Public Resource View Openfid Php Id 63



Http Www Topmath Org J Student Pdf




怎麼知道的 紅線 Clear



三元一次方程式求連比 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌




用matlab 0 Cript解聯立方程式 Labview Labview360論壇




1 4例題3三元一次聯立方程式的無限多解 Youtube




隨筆誌 二下2 3三元一次聯立方程式比例式解題想法



名師課輔網 聯立方程式的解




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




4 2 3三元一次聯立方程式




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




例題 解二元一次聯立方程式 綜合應用2 數學 均一教育平台




Mathematics 数学分享站 解三元一次联立方程式 Facebook



課業輔導中心 2 3 三元一次聯立方程組p 85




隨筆誌 二下2 3三元一次聯立方程式 克拉瑪法則證明




翻轉學習影片 高中 數學 三元一次聯立方程組 練習13



若二元一次聯立方程式5 Y 5 阿摩線上測驗



Http Ccnt4 Cute Edu Tw Huili1022 102 2 N7 Pdf




二元一次方程式題型 大家都在找解答 訂房優惠報報
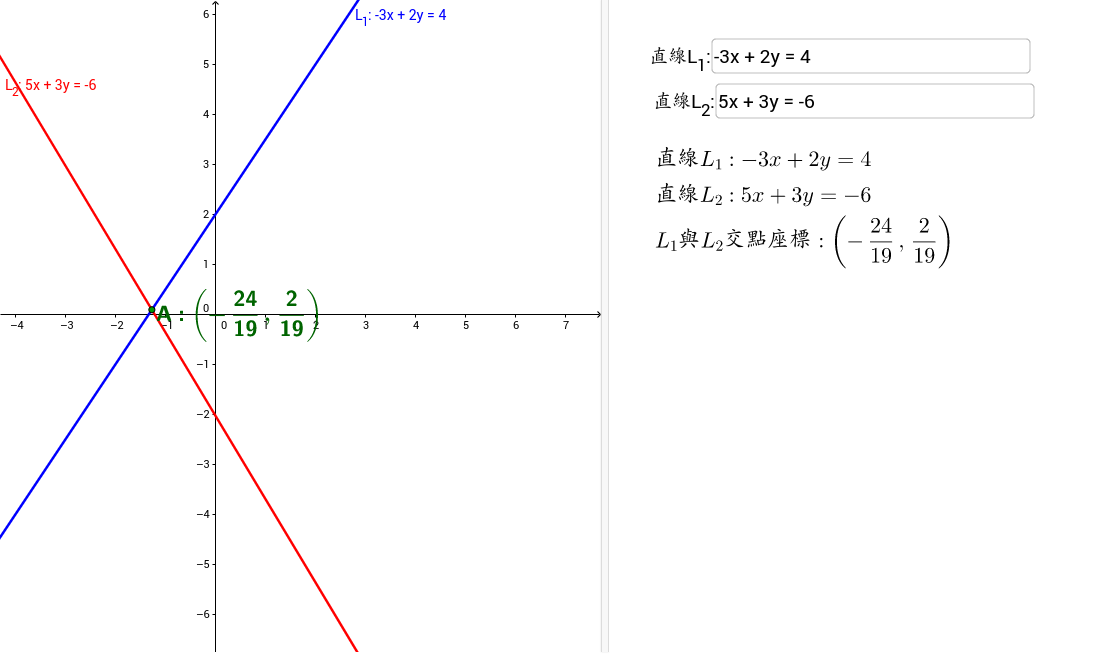



二元一次聯立方程式圖解 Geogebra




方程組 維基百科 自由的百科全書




求解 這兩題我不會 Clear




3 3克拉瑪公式




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



三元一次聯立方程式 由未知數討論方程組的解 Youtube




二元一次聯立方程式無解 大家都在找解答 第2頁 Nbsp Nbsp 訂房優惠報報




6 3 联立方程计量经济学模型的识别 Ppt 6 3 联立方程计量经济学模型的识 The Identification Problem 一 识别的概念 Course Hero



1




Ppt 2 2 二元一次方程式的圖形powerpoint Presentation Free Download Id



100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




求高手我這三題真的無法這是二元一次聯立方程式應用覺得難 Clear




三元一次聯立方程式 利用克拉瑪公式判斷三平面關係之一 Youtube




重新載圖3 小柯以代入消去法解二元一次聯立方程式 計算步驟如下 請問小柯從哪一 阿摩線上測驗
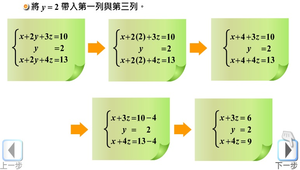



高斯消去法解三元一次聯立方程式




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




怎麼知道的 紅線 Clear



聯立方程 教育多媒體



三元一次方程式excel 40 三元一次聯立方程式的公式解 克拉瑪公式的說明 Mtlpe



联立方程式 快懂百科




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア
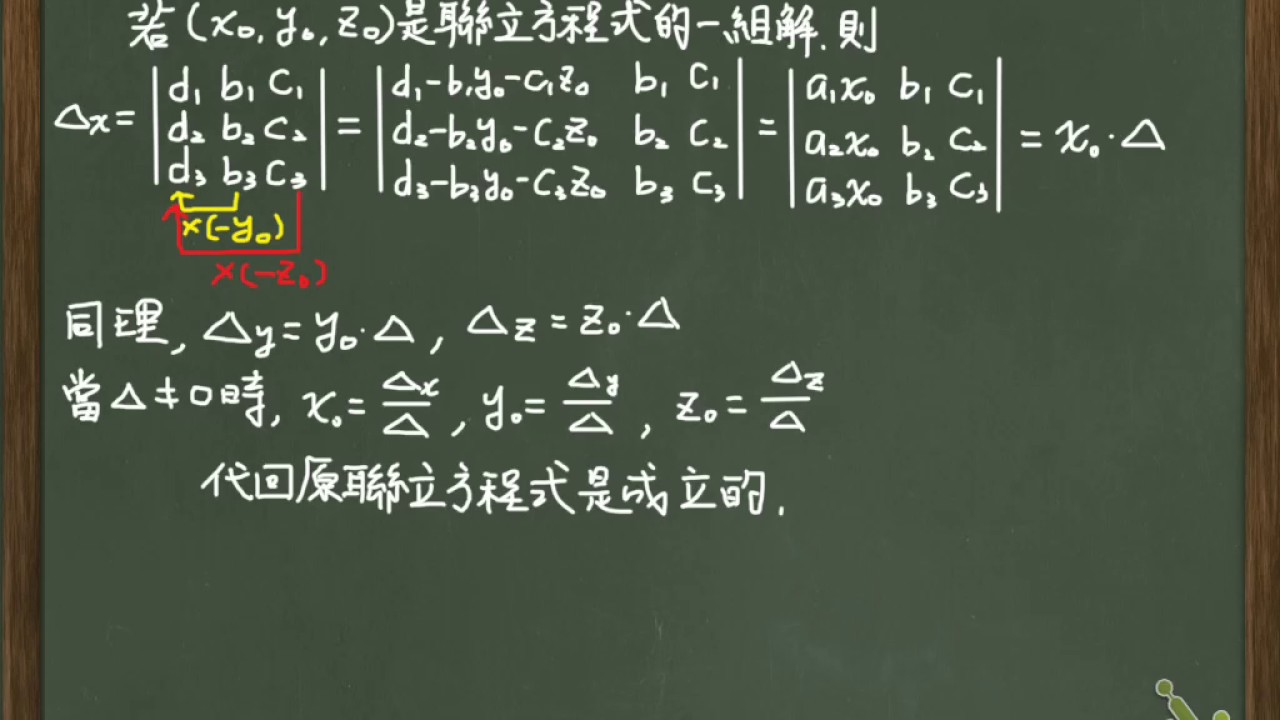



40 三元一次聯立方程式的公式解 克拉瑪公式的說明 Youtube



Http Www Topmath Org Jtest Ex 0602 Pdf



Q Tbn And9gcsm6 Ygdifx7pydebyfkxkcficln0q2usbh7vlhkbagbczf8kws Usqp Cau



6 5 聯立方程式聯立方程式求三階 列式15 01 1974 7 3 4 5 2 3 之值 求三階 列式99 9 7 199 4 3 29




翻轉學習影片 高中 數學 三元一次聯立方程組 練習3




4 2 3三元一次聯立方程式



Http Www Math Nsysu Edu Tw Outstanding Use Report 1007 Pdf




國中數學學思達講義 二元一次聯立方程式 Shareclass



Priori Moe Gov Tw Download Textbook Math Grade7 Book2 Math 7 2 3 1 Pdf




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




高二高中數學的 數甲 B4 2 3 三元一次聯立方程式筆記 Clear



6 3 聯立方程式聯立方程式求行列式6 8 2 15 5 3 4 1 之值 求行列式15 10 15 15 0 6 2 6 4



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




翻轉學習影片 高中 數學 三元一次聯立方程組 練習10




如何用三元一次聯立方程式 解姚文智 沉默螺旋民調再加15 問題 The News Lens 關鍵評論網



測評網 國一下 數學第一次段考 複習錦囊



Http K12 Camdemy Com Sysdata Doc 2 23e36ac63 Pdf Pdf
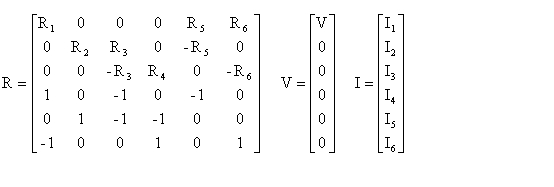



Matlab方程式求解 Ytffhew的博客 程序员宅基地 Matlab方程式求解 程序员宅基地



2



聯立方程式餐坊 台灣公司網




二元一次方程組練習題不會 來看看二元一次方程組知識點 每日頭條




隨筆誌 一下1 2解二元一次聯立方程式 指數問題



克拉瑪公式解三元一次方程組 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌




联立方程是几年级学的 西瓜视频



測評網 國一下 數學第一次段考 複習錦囊
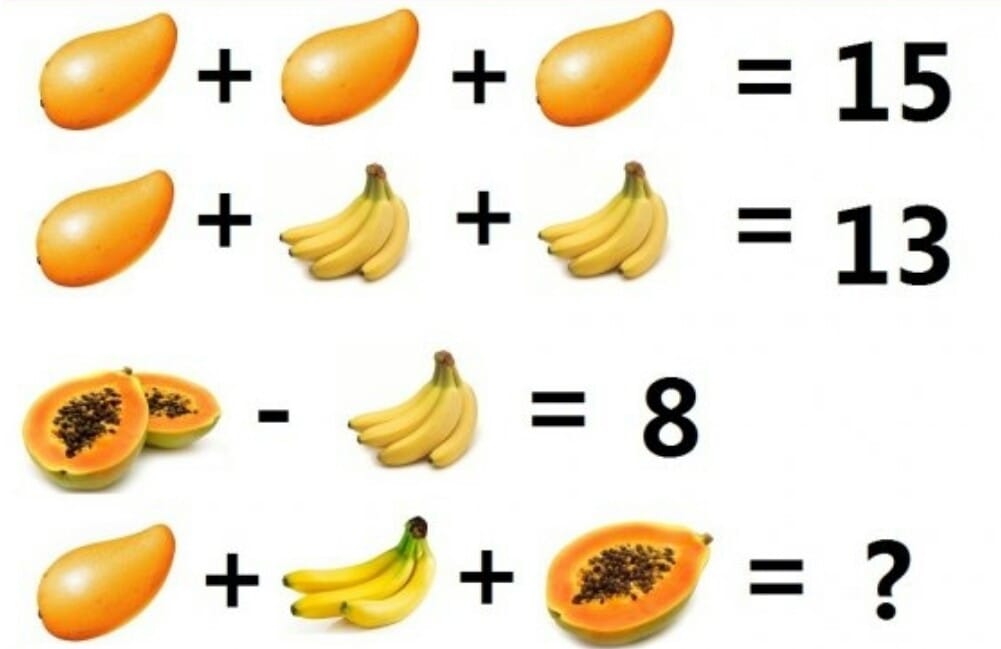



大家來解謎 解二元一次聯立方程式 導入活動 環遊數界



Http Www Ycvs Ntpc Edu Tw Ezfiles 0 1000 Img 125 Ch1 1 Pdf




三元一次聯立方程式 克拉瑪公式說明 Youtube



Q Tbn And9gcr6cto4p7dzcq6zf K9artmgeytohwxvgynmlrwpcdi2wifi1eg Usqp Cau




Ok423 三元一次連立方程組1 Ok423 三元一次聯立方程式主題一解聯立方程式1 可用加減消去法或代入消去法求解 2 聯立方程式的解可分成三種 1 恰有一解 2 無限多組解 3 無解 Pdf 免费下载



2




大家來解謎 解二元一次聯立方程式 導入活動 環遊數界



測評網 國一下 數學第一次段考 複習錦囊




例題 加減消去法2 解二元一次聯立方程式 均一教育平台



コメント
コメントを投稿